Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
Can you solve help show the sets for the questions:
![**Transcription for Educational Website**
**Title:** Listing Elements of Given Sets
**Description:**
For each of the following mathematical expressions, list all the elements of the set provided between braces.
**Set Expressions:**
(a) \[\bigcap_{n \in \mathbb{N}} \left\{ x \in \mathbb{R} : 3 - \frac{1}{n} \leq x \leq 3 + \frac{1}{n} \right\}.\]
- Explanation: This set represents the intersection of intervals centered at 3 with rapidly decreasing widths as \(n\) increases. As \(n\) approaches infinity, \(\frac{1}{n}\) approaches zero, causing the interval \([3 - \frac{1}{n}, 3 + \frac{1}{n}]\) to shrink towards the point 3.
(b) \[\bigcup_{n \in \mathbb{N}} \left\{ x \in \mathbb{R} : 3 - \frac{1}{n} \leq x \leq 3 + \frac{1}{n} \right\}.\]
- Explanation: This set is the union of similar intervals as in (a), covering every real number between 2 and 4, because as \(n\) increases, each interval expands, converging to the open interval (2, 4).
(c) \[\{ X \subseteq \{ x, y, z, w \} : |\mathcal{P}(X)| = 8 \}\]
- Explanation: Here, the set \(X\) is a subset of \(\{x, y, z, w\}\) with the condition that the power set \(\mathcal{P}(X)\) has exactly 8 elements. This condition implies that \(X\) must have 3 elements, because a set with \(k\) elements has a power set of size \(2^k\).
(d) \[\{ X \subseteq \mathcal{P}(\{ 1, 2, 3 \}) : |X| \leq 1 \}\]
- Explanation: This set contains subsets \(X\) of the power set of \(\{1, 2, 3\}\) where \(X\) can have at most 1](https://content.bartleby.com/qna-images/question/68cbddc0-dc01-4c42-ad75-db2c7bdfa41f/23414dd9-366a-41c1-86dc-7899d019f1e7/3me8wx8k_processed.png)
Transcribed Image Text:**Transcription for Educational Website**
**Title:** Listing Elements of Given Sets
**Description:**
For each of the following mathematical expressions, list all the elements of the set provided between braces.
**Set Expressions:**
(a) \[\bigcap_{n \in \mathbb{N}} \left\{ x \in \mathbb{R} : 3 - \frac{1}{n} \leq x \leq 3 + \frac{1}{n} \right\}.\]
- Explanation: This set represents the intersection of intervals centered at 3 with rapidly decreasing widths as \(n\) increases. As \(n\) approaches infinity, \(\frac{1}{n}\) approaches zero, causing the interval \([3 - \frac{1}{n}, 3 + \frac{1}{n}]\) to shrink towards the point 3.
(b) \[\bigcup_{n \in \mathbb{N}} \left\{ x \in \mathbb{R} : 3 - \frac{1}{n} \leq x \leq 3 + \frac{1}{n} \right\}.\]
- Explanation: This set is the union of similar intervals as in (a), covering every real number between 2 and 4, because as \(n\) increases, each interval expands, converging to the open interval (2, 4).
(c) \[\{ X \subseteq \{ x, y, z, w \} : |\mathcal{P}(X)| = 8 \}\]
- Explanation: Here, the set \(X\) is a subset of \(\{x, y, z, w\}\) with the condition that the power set \(\mathcal{P}(X)\) has exactly 8 elements. This condition implies that \(X\) must have 3 elements, because a set with \(k\) elements has a power set of size \(2^k\).
(d) \[\{ X \subseteq \mathcal{P}(\{ 1, 2, 3 \}) : |X| \leq 1 \}\]
- Explanation: This set contains subsets \(X\) of the power set of \(\{1, 2, 3\}\) where \(X\) can have at most 1
Expert Solution
arrow_forward
Step 1
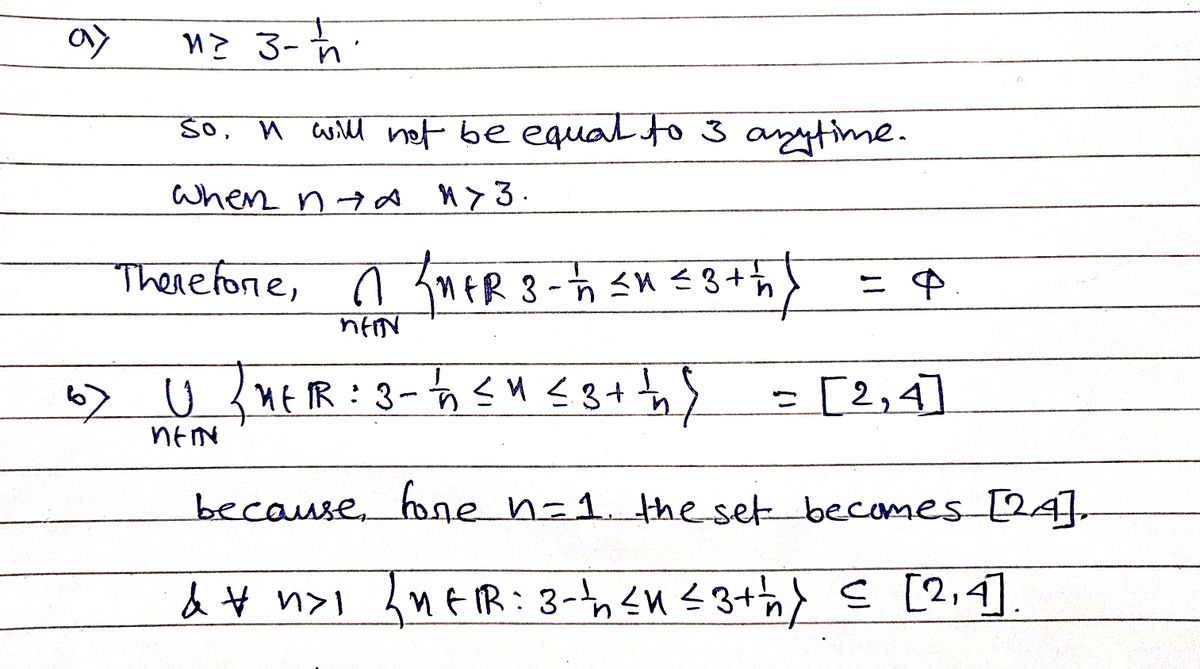
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,