Question
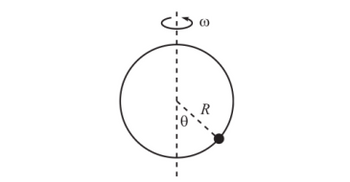
A mass m is free to move without friction in a hoop of radius R, which has no mass. The hoop rotates with a constant
(a) Write the Lagrangian of the system as a function of θ.
(b) Find the equation of motion for mass m.
(c) Determine the equilibrium angles, that is, the conditions for which
˙θ = ¨θ = 0 .
Consider two cases: ω² ≥ g/R and ω² < g/R.
Transcribed Image Text:$
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- (a) The magnitude of the angular momentum about the origin of a particle of mass m moving with velocity v on a path that is a perpendicular distance d from the origin is given by m/v|d. Show that if r is the position of the particle then the vector J =r × mv represents the angular momentum. (b) Now consider a rigid collection of particles (or a solid body) rotating about an axis through the origin, the angular velocity of the collection being represented by w. (i) Show that the velocity of the ith particle is Vi = w X ri and that the total angular momentum J is J = Σm₁ [r}w - (r; · w)r;]. (ii) Show further that the component of J along the axis of rotation can be written as Iw, where I, the moment of inertia of the collection about the axis or rotation, is given by 1 = Σm₁p². Interpret pi geometrically. (iii) Prove that the total kinetic energy of the particles is 1².arrow_forwardWrite down the inertia tensor for a square plate of side ? and mass ? for a coordinate system with origin at the center of the plate, the z-axis being normal to the plate, and the x- and y- axes parallel to the edges.arrow_forwardEngineering Dynamics need help from 4,5,6,7 thank you A ball of mass m is moving along a vertical semi-cylinder of radius R as it is guided by the arm OA. The arm moves in a clockwise direction with a constant angular velocity ω. Assume 0° ≤ Φ ≤ 90°. Neglect any friction. Neglect also the size of the ball and the thickness of the arm. Find the relationship between r, R and θ where r is the distance between O and the ball. Draw a free body diagram of the ball assuming that it is in contact with the cylinder and the arm OA. Write the equations of motion in the (r, θ) coordinate system. Find the normal force acting on the ball by the cylinder for Φ = Φ0. Find the normal force acting on the ball by the bar for Φ = Φ0. Determine the angle Φ at which the ball loses contact with the cylinder. Take m = 1 kg, R = 1.4 m, ω = 0.5 rad/s, and Φ = 60°arrow_forward
- Consider the “Foucault pendulum”, as shown below. Foucault set up his 1851 spherical pendulum (of mass m and length L) experiment in the Pantheon dome of Paris, showing that the plane of oscillation rotates and takes about 1.3 days to fully revolve around. This demonstrated the extent to which Earth’s surface is not an inertial reference frame (e.g., role of the Coriolis force). Your task here is to determine (but not solve) the equations of motion.arrow_forwardA particle of mass m is located at x = 1, y = 0,2 = 2. Find the tensor of inertia for the particle relative to the origin. The particle rotates about the z axis through a small angle a <<1 as shown below. Show that the moments of inertia are unchanged to second order in a but the products of inertia can change linearly with a.arrow_forwardFor the pipe assembly of Prob. 4.101, determine (a) the largest permissible value of a if the assembly is not to tip, (b) the corresponding tension in each wire.(Reference to Problem 4.101):Two steel pipes AB and BC , each having a mass per unit length of 8 kg/m, are welded together at B and supported by three vertical wires. Knowing that a= 0.4 m, determine the tension in each wire.arrow_forward
arrow_back_ios
arrow_forward_ios