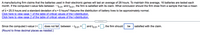
A manufacturing firm claims that the batteries used in their electronic games will last an average of 28 hours. To maintain this average, 16 batteries are tested eachmonth. If the computed t-value falls between - to 01 and to 01, the firm is satisfied with its claim. What conclusion should the firm draw from a sample that has a meanof x = 25.5 hours and a standard deviation of s = 5 hours? Assume the distribution of battery lives to be approximately normal.Click here to view page 1 of the table of critical values of the t-distribution.Click here to view page 2 of the table of critical values of the t-distribution......Since the computed t-value t=does not fall between - to.01and to.01%3Dthe firm shouldbesatisfied with the claim.(Round to three decimal places as needed.)

Answered: Image /qna-images/answer/bd9f59f5-06b1-4f11-8ae8-8a2e3db378d9.jpg

Answered: A manufacturing firm claims that the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

A person's blood glucose level and diabetes are closely related. Let x be a random variable measured in milligrams of glucose per deciliter (1/10 of a liter) of blood. Suppose that after a 12-hour fast, the random variable x will have a distribution that is approximately normal with mean = 88 and standard deviation = 21. Note: After 50 years of age, both the mean and standard deviation tend to increase. For an adult (under 50) after a 12-hour fast, find the following probabilities. (Round your answers to four decimal places.) g USE SALT (a) x is more than 60 (b) x is less than 110. (c) x is between 60 and 110. (d) x is greater than 125 (borderline diabetes starts at 125)
A person's blood glucose level and diabetes are closely related. Let x be a random variable measured in milligrams of glucose per deciliter (1/10 of a liter) of blood. Suppose that after a 12-hour fast, the random variable x will have a distribution that is approximately normal with mean u = 86 and standard deviation o = 26. Note: After 50 years of age, both the mean and standard deviation tend to increase. For an adult (under 50) after a 12-hour fast, find the following probabilities. (Round your answers to four decimal places.) A USE SALT (a) x is more than 60 0.8315 (b) x is less than 110 (c) x is between 60 and 110 (d) x is greater than 125 (borderline diabetes starts at 125)
Suppose that for the past several decades, daily precipitation in Seattle, Washington has had a mean of 2.4 mm and a standard deviation of 11.4 mm. Researchers suspect that in recent years, the mean amount of daily precipitation has changed, so they plan to obtain data for a random sample of 195 days over the past five years and use this data to conduct a one-sample ?z‑test of ?0:?=2.4H0:μ=2.4 mm against ?1:?≠2.4H1:μ≠2.4 mm, where ?μ is the mean daily precipitation for the last five years. Although they realize that rainfall does not follow a normal distribution, they feel safe using a ?z‑test because the sample size is large. The researchers want to know what the power of this test is to reject the null hypothesis at significance level ?=0.05α=0.05 if the actual mean daily precipitation is 2.6 mm or more. Computing power by hand requires two steps. The first step is to use a significance level of 0.05 to determine the values of the sample mean for which they will reject their null…
For a sample with a standard deviation of s=4, a score of X=35 corresponds to Z= -1.25. what is the sample mean?
In a sample of 14 randomly selected high school seniors, the mean score on a standardized test was 1197 and the standard deviation was 166.9. Further research suggests that the population mean score on this test for high school seniors is 1018. Does the t-value for the original sample fall between -to.95 and to.95? Assume that the population of test scores for high school seniors is normally distributed. fall between -to.95 and to.95 because to.95 = The t-value of t= (Round to two decimal places as needed.) C
Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 3000 grams and a standard deviation of 900 grams while babies born after a gestation period of 40 weeks have a mean weight of 3300 grams and a standard deviation of 420 grams. If a 34-week gestation period baby weighs 2500 grams and a 41-week gestation period baby weighs 2800 grams, find the corresponding z-scores. Which baby weighs less relative to the gestation period? Find the corresponding z-scores. Which baby weighs relatively less? Select the correct choice below and fill in the answer boxes to complete your choice. (Round to two decimal places as needed.) OA. The baby born in week 41 weighs relatively less since its z-score, baby born in week 34. OB. The baby born in week 34 weighs relatively less since its z-score, baby born in week 41. OC. The baby born in week 41 weighs relatively less since its z-score, baby born in week 34. OD. The baby born in week 34 weighs [relatively less since its…
In a random sample of 6 cell phones, the mean full retail price was $547.30 and the standard deviation was $176.00. Further research suggests that the population mean is $428.25. Does the t-value for the original sample fall between and to.95? Assume that the population of full retail prices for cell phones is normally distributed. - to.95 The t-value of t = fall between -1 -to.95 and to. .95 because to 95 = (Round to two decimal places as needed.)
Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 2500 grams and a standard deviation of 800 grams while babies born after a gestation period of 40 weeks have a mean weight of 3000 grams and a standard deviation of 385 grams. If a 32-week gestation period baby weighs 2650 grams and a 41-week gestation period baby weighs 3150 grams, find the corresponding z-scores. Which baby weighs more relative to the gestation period? Find the corresponding z-scores. Which baby weighs relatively more? Select the correct choice below and fill in the answer boxes to complete your choice. (Round to two decimal places as needed.) A. The baby born in week 41 weighs relatively more since its z-score, nothing, is smaller than the z-score of nothing for the baby born in week 32. B. The baby born in week 32 weighs relatively more since its z-score, nothing, is smaller than the z-score of nothing for the baby born in week 41. C. The…
Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 2900 grams and a standard deviation of 600 grams while babies born after a gestation period of 40 weeks have a mean weight of 3100 grams and a standard deviation of 505 grams. If a 32-week gestation period baby weighs 2575 grams and a 41-week gestation period baby weighs 2775 grams, find the corresponding z-scores. Which baby weighs less relative to the gestation period? Find the corresponding z-scores. Which baby weighs relatively less? Select the correct choice below and fill in the answer boxes to complete your choice. (Round to two decimal places as needed.) O A. The baby born in week 32 weighs relatively less since its z-score, smaller than the z-score of for the baby born in week 41. OB. The baby born in week 32 weighs relatively less since its z-score, larger than the z-score of for the baby born in week 41. OC. The baby born in week 41 weighs relatively less since its z-score, larger than the…
Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 2500 grams and a standard deviation of 700 grams while babies born after a gestation period of 40 weeks have a mean weight of 2700 grams and a standard deviation of 340 grams. If a 34-week gestation period baby weighs 2275 grams and a 40-week gestation period baby weighs 2475 grams, find the corresponding z-scores. Which baby weighs less relative to the gestation period?
Suppose babies born after a gestation period of 32 to 35 weeks have a mean weight of 3000 grams and a standard deviation of 1000 grams while babies born after a gestation period of 40 weeks have a mean weight of 3500 grams and a standard deviation of 545 grams. If a 35-week gestation period baby weighs 3300 grams and a 41-week gestation period baby weighs 3800 grams, find the corresponding z-scores. Which baby weighs more relative to the gestation period? ..... Find the corresponding z-scores. Which baby weighs relatively more? Select the correct choice below and fill in the answer boxes to complete your choice. (Round to two decimal places as needed.) A. The baby born in week 41 weighs relatively more since its z-score, is larger than the z-score of for the baby born in week 35. O B. The baby born in week 35 weighs relatively more since its z-score, is larger than the z-score of for the baby born in week 41. C. The baby born in week 41 weighs relatively more since its z-score, is…
A person's blood glucose level and diabetes are closely related. Let x be a random variable measured in milligrams of glucose per deciliter (1/10 of a liter) of blood. Suppose that after a 12-hour fast, the random variable x will have a distribution that is approximately normal with mean ? = 81 and standard deviation ? = 26. Note: After 50 years of age, both the mean and standard deviation tend to increase. For an adult (under 50) after a 12-hour fast, find the following probabilities. (Round your answers to four decimal places.) (a) x is more than 60(b) x is less than 110(c) x is between 60 and 110(d) x is greater than 125 (borderline diabetes starts at 125)

SEE MORE QUESTIONS

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS