A LED lamp is used to do Young’s double slit interference experiment. The slit separation d = 0.02 mm. On the screen behind, it is found that the distance between first order maximum of green light (532 nm) and second order minimum of red light (643 nm) is Δy =15 cm. Find the distance between slit and screen S.
A LED lamp is used to do Young’s double slit interference experiment. The slit separation d = 0.02 mm. On the screen behind, it is found that the distance between first order maximum of green light (532 nm) and second order minimum of red light (643 nm) is Δy =15 cm. Find the distance between slit and screen S.
Related questions
Question
A LED lamp is used to do Young’s double slit interference experiment. The slit separation d = 0.02 mm. On the screen behind, it is found that the distance between first order maximum of green light (532 nm) and second order minimum of red light (643 nm) is
Δy =15 cm. Find the distance between slit and screen S.
Transcribed Image Text:Ay
YR
YG
ODark
OBright
d = 0.02 mm
{
S = ?
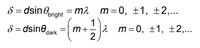
Transcribed Image Text:8 = dsinegricht = m2
m = 0, ±1, ±2,...
1
8 = dsine,
|2 m=0, ±1, ±2,...
m+
dark
2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps
