Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 2MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 3MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 4MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 5MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 6MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 7MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 8MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 9MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 10MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 11MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 12MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 13MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 14MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 15MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 16MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 17MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 18MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 19MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 20MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 21MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 22MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 23MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 24MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 25MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,... Problem 26MCCP: 26. List all the rational numbers in this set:
.
Problem 27MCCP: In Exercises 27-28, rewrite each expression without absolute value bars. | 213 | Problem 28MCCP Problem 29MCCP: 29. If the population of the United States is approximately and each person produces about 4.6... Problem 30MCCP: A human brain contains 31010 neurons and a gorilla brain contains 7.5109 neurons. How many times as... Problem 31MCCP: College students arc graduating with the highest debt burden in history. The bar graph shows the... Problem 1RE: In Exercises 1-2, evaluate each algebraic expression for the given value or values of the... Problem 2RE: In Exercises 1-2, evaluate each algebraic expression for the given value or values of the... Problem 3RE: You are riding along an expressway traveling x miles per hour. The formula S=0.015x2+x+10 models the... Problem 4RE Problem 5RE Problem 6RE Problem 7RE: 7.
In Exercises 4-7, let . And . Find the indicated set.
Problem 8RE Problem 9RE Problem 10RE Problem 11RE: In Exercises 9-11, rewrite each expression without absolute value bars.
11.
Problem 12RE: 12. Express the distance between the numbers -17 and 4 using absolute value. Then evaluate the... Problem 13RE: In Exercises 13-18, state the name of the property illustrated.
13.
Problem 14RE Problem 15RE Problem 16RE Problem 17RE Problem 18RE Problem 19RE Problem 20RE: In Exercises 19-22, simplify each algebraic expression 15(5x)+[(3y)+(3y)](x) Problem 21RE Problem 22RE Problem 23RE Problem 24RE: Evaluate each exponential expression in Exercises (3)3(2)2 Problem 25RE Problem 26RE Problem 27RE Problem 28RE Problem 29RE: Simplify each exponential expression in Exercises 28-31.
29.
Problem 30RE Problem 31RE Problem 32RE: In Exercises 32-33, write each number in decimal notation.
32.
Problem 33RE Problem 34RE Problem 35RE Problem 36RE Problem 37RE Problem 38RE: In 2009, the United States government spent more than it had collected in taxes, resulting in a... Problem 39RE Problem 40RE Problem 41RE Problem 42RE Problem 43RE: Use the product rule to simplify the expressions in Exercises 41-44.In Exercises 43-44, assume that... Problem 44RE Problem 45RE Problem 46RE Problem 47RE: In Exercises 47-49, add or subtract terms whenever possible.
47.
Problem 48RE Problem 49RE Problem 50RE Problem 51RE Problem 52RE Problem 53RE Problem 54RE Problem 55RE: Evaluate each expression in Exercises 54-57 or indicate that the root is not a real number. 325 Problem 56RE Problem 57RE Problem 58RE: Simplify the radical expressions in Exercises 58-62. 813 Problem 59RE Problem 60RE Problem 61RE: Simplify the radical expressions in Exercises 58-62. 4163+523 Problem 62RE Problem 63RE Problem 64RE Problem 65RE Problem 66RE Problem 67RE: In Exercises 63-68, evaluate each expression. 6423 Problem 68RE Problem 69RE Problem 70RE Problem 71RE: In Exercises 69-71, simplify using properties of exponents.
71.
Problem 72RE Problem 73RE: In Exercises 73-74, perform the indicated operations. Write the resulting polynomial in standard... Problem 74RE: In Exercises 73-74, perform the indicated operations. Write the resulting polynomial in standard... Problem 75RE Problem 76RE Problem 77RE Problem 78RE Problem 79RE Problem 80RE Problem 81RE Problem 82RE: In Exercises 82-83, perform the indicated operations. Indicate the degree of the resulting... Problem 83RE: In Exercises 82-83, perform the indicated operations. Indicate the degree of the resulting... Problem 84RE: In Exercises 84-88, find each product. (x+7y)(3x5y) Problem 85RE: In Exercises 84-88, find each product.
85.
Problem 86RE Problem 87RE Problem 88RE: In Exercises 84-88, find each product. (ab)(a2+ab+b2) Problem 89RE Problem 90RE: In Exercises 89-105, factor completely, or state that the polynomial is prime. x211x+28 Problem 91RE Problem 92RE Problem 93RE Problem 94RE Problem 95RE Problem 96RE Problem 97RE Problem 98RE Problem 99RE Problem 100RE: In Exercises 89-105, factor completely, or state that the polynomial is prime. x3+64 Problem 101RE Problem 102RE Problem 103RE Problem 104RE: In Exercises 89-105, factor completely, or state that the polynomial is prime.
104.
Problem 105RE Problem 106RE: In Exercises 106-108, factor and simplify each algebraic expression.
106.
Problem 107RE: In Exercises 106-108, factor and simplify each algebraic expression. (x24)(x2+3)12(x24)2(x2+3)32 Problem 108RE Problem 109RE Problem 110RE Problem 111RE: In Exercises 109-111, simplify each rational expression. Also, list all numbers that must be... Problem 112RE Problem 113RE Problem 114RE Problem 115RE: In Exercises 115-118, add or subtract as indicated.
115.
Problem 116RE: In Exercises 115-118, add or subtract as indicated. 3xx+2+xx2 Problem 117RE: In Exercises 115-118, add or subtract as indicated. xx29+x1x25x+6 Problem 118RE: In Exercises 115-118, add or subtract as indicated.
118.
Problem 119RE: In Exercises 119-121, simplify each complex rational expression. 1x1213x6 Problem 120RE Problem 121RE Problem 1T: In Exercises 1-18, simplify the given expression or perform the indicated operation (and simplify,... Problem 2T: In Exercises 1-18, simplify the given expression or perform the indicated operation (and simplify,... Problem 3T: In Exercises 1-18, simplify the given expression or perform the indicated operation (and simplify,... Problem 4T Problem 5T: In Exercises 1-18, simplify the given expression or perform the indicated operation (and simplify,... Problem 6T Problem 7T Problem 8T Problem 9T Problem 10T Problem 11T Problem 12T Problem 13T Problem 14T Problem 15T Problem 16T Problem 17T: In Exercises 1-18, simplify the given expression or perform the indicated operation (and simplify,... Problem 18T Problem 19T: In Exercises 19-24, factor completely, or state that the polynomial is prime. x29x+18 Problem 20T Problem 21T: In Exercises 19-24, factor completely, or state that the polynomial is prime. 25x29 Problem 22T: In Exercises 19-24, factor completely, or state that the polynomial is prime. 36x284x+49 Problem 23T: In Exercises 19-24, factor completely, or state that the polynomial is prime.
23.
Problem 24T Problem 25T: 25. Factor and simplify:
Problem 26T: 26. List all the rational numbers in this set:
.
Problem 27T Problem 28T: In Exercises 27-28, state the name of the property illustrated. Problem 29T: Express in scientific notation: 0.00076. Problem 30T Problem 31T Problem 32T: Big (Lack of) Men on Campus In 2007, 135 women received bachelor's degrees for every 100 men.... format_list_bulleted
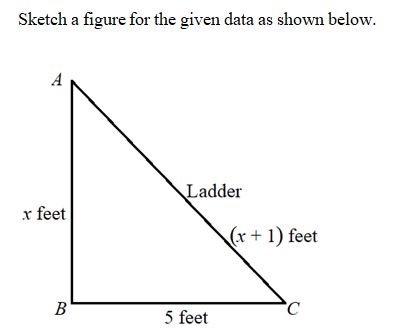
![**Problem Description:**
A ladder leans against a wall so that the base of the ladder is 5 feet from the wall. If the vertical height reached by the ladder along the wall is x feet and the length of the ladder is 1 foot more than the vertical height, find the length of the ladder.
**Explanation and Steps:**
1. **Identify Known Values:**
- Distance from the wall to the base of the ladder (Adj) = 5 feet.
- Vertical height reached by the ladder (Opp) = x feet.
- Length of the ladder (Hyp) = x + 1 feet.
2. **Apply the Pythagorean Theorem:**
The Pythagorean Theorem states that in a right-angled triangle:
\[
\text{(Hypotenuse)}^2 = \text{(Opposite side)}^2 + \text{(Adjacent side)}^2
\]
Substitute the known values:
\[
(x + 1)^2 = x^2 + 5^2
\]
3. **Simplify the Equation:**
Expand and simplify the equation:
\[
x^2 + 2x + 1 = x^2 + 25
\]
4. **Solve for x:**
Subtract \(x^2\) from both sides of the equation:
\[
2x + 1 = 25
\]
\[
2x = 24
\]
\[
x = 12
\]
5. **Find the Length of the Ladder:**
The length of the ladder = \(x + 1\):
\[
x + 1 = 12 + 1 = 13
\]
**Answer:**
The length of the ladder is 13 feet.](https://content.bartleby.com/qna-images/question/d5dead9f-e821-4d1f-b49e-a22938bc1d4f/59f9efff-529f-405f-9109-49e909502d8a/lgx117_reoriented.jpeg)
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education