
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:Suppose \( f: A \rightarrow B \) is a non-zero group homomorphism. Which of the following are true?
(i) If \( A = \mathbb{Z}_{36}, B = \mathbb{Z}_{6}, f(2) = 4 \), then \( f(10) = 2 \).
(ii) If \( A = B = \mathbb{Z}_{20}, f(7) = 9 \), then \( f(1) = 6 \).
(iii) If \( f \) is an isomorphism, then \(\ker(f) \neq \{e\}\).
(iv) If \( A = U_{10}, B = \mathbb{Z}_{4}, f(3) = 2 \), then \(\ker(f) = \{1\}\).
Options:
- A: (ii), (iii)
- B: (i), (ii)
- C: (i)
- D: (iv)
- E: (i), (iv)
Expert Solution
arrow_forward
Step 1
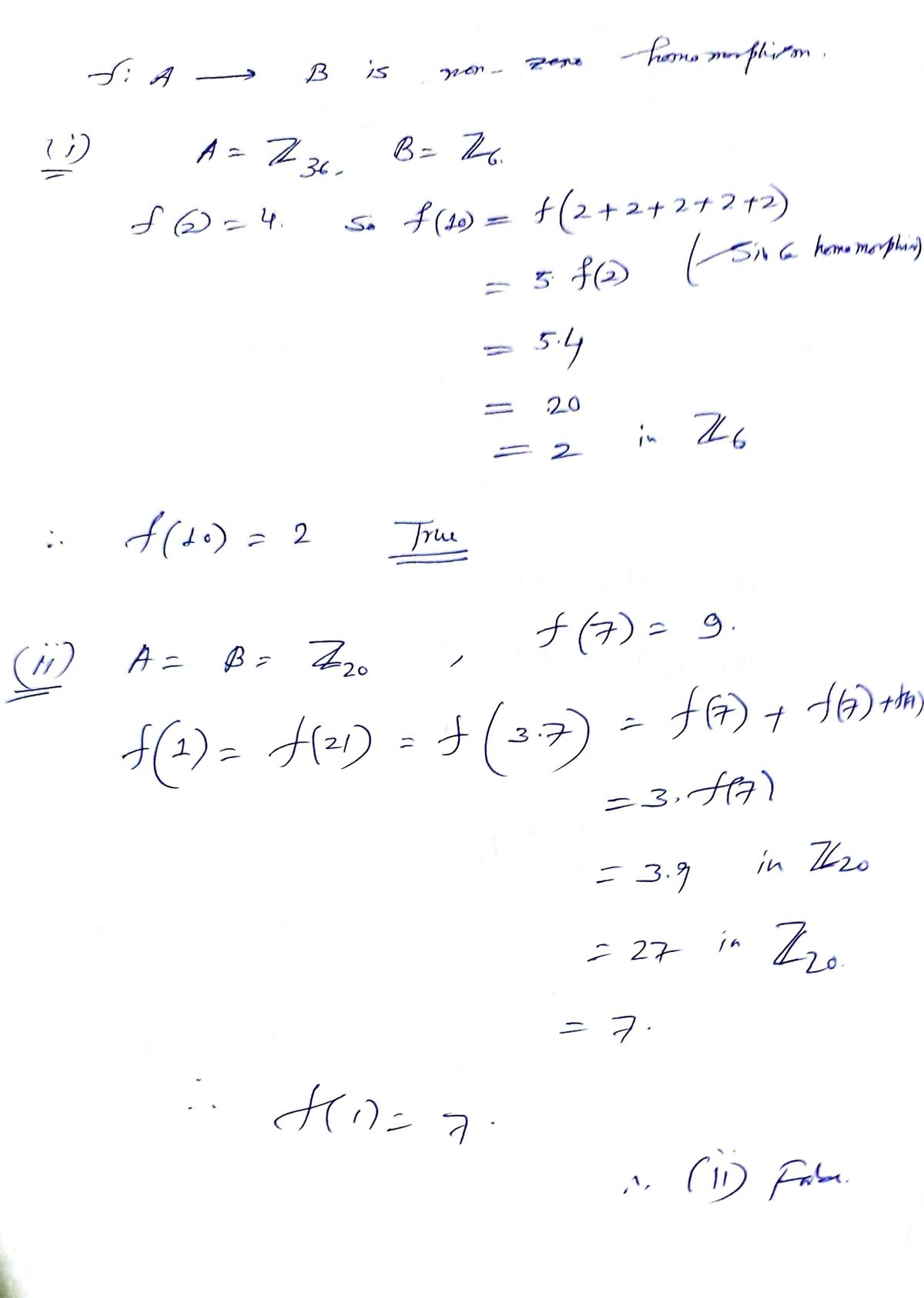
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- please be as thorough as you can. When finished please provide 2-3 examples. Please.arrow_forward1. Consider the group U(5).(a) What is |U(5)|?(b) For each a ∈ U(5), find |a|, < a >, and | < a > | 2. Consider the group Z6.(a) What is Z6?(b) For each a ∈ Z6, find |a|, < a >, and | < a > |.arrow_forward(4) Chapter 2, exercise 6.9: Prove that a group and its opposite group Gº (Exercise 2.6) are isomorphic.arrow_forward
- inf (A) Give the example that group A is not null and -00 = and (sup (A) = max (A). - Sarrow_forwardHello, can you help me out with this problem? Please write a solution on a piece of paper and upload it here. Introduction of the problem: Let G = ℤ32 and H be the group of G generated by 4 Problem: What is (3 + H)-1 in G/H?arrow_forwardFind the order of the element 2+ (6) in the group Z30/(6).arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

