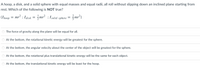
A hoop, a disk, and a solid sphere with equal masses and equal radii, all roll without slipping down an inclined plane starting from rest. Which of the following is NOT true? (I hoop mr? ; Idisk zmr² ; Isolid sphere = žmr²) O The force of gravity along the plane will be equal for all. O At the bottom, the rotational kinetic energy will be greatest for the sphere. O At the bottom, the angular velocity about the center of the object will be greatest for the sphere. O At the bottom, the rotational plus translational kinetic energy will be the same for each object. O At the bottom, the translational kinetic energy will be least for the hoop.

A ball that is a uniformly hollow spherical shell with a mass of m and radius r rolls down an inclined plan without slipping. The inclined plane is at an angle theta from horizontal and has a length L. What is the speed at the bottom for the ball?

solve for Part D

Apply error propagation to determine the associated uncertainty in the average volume… Plz

A solid cylinder of radius R rolls without slipping on a horizontal plane. The velocity of its CM is V=2m/s. Then the cylinder rolls uphill, also without slipping. What maximal height h, will the cylinder reach? plz show step by step on how you acquired the formula you are using for this problem!!! Thank You

A ball of mass 5.5 kg is released from rest from the top of a 4.0 m long hill that is inclined at 30°, as shown in figure. The ball rolls along the hill without slipping. The rotational inertia of a sphere of mass M and radius R about its center of mass is MR. (cos 30° = 0.866, sin 30° = 0.5, g = 9.8m/s?) a) Calculate the force due to friction acting on the ball as it rolls along the hill, b) Calculate the linear speed of the center of mass of the ball when it reaches the bottom edge of the hill, c) A wagon containing a box is at rest on the ground below the hill so that the ball falls the vertical distance of 3.0 m and lands and sticks in the center of the box. The total mass of the wagon and the box is 12 kg. Calculate the horizontal speed of the wagon immediately after the ball lands in it. 4,0 m 3.0 m

A В C A cylindrical object rolls without slipping down a ramp and around a loop-the-loop as shown in the figure above. The object maintains contact with the ramp and loop at all times. At position B, (just after passing the top part of the loop) what direction is the angular acceleration of the cylinder? Up and to the right Down and to the left Down and to the right Towards the center of the circle Downward Into the page Out of the page

A long, thin uniform rod of length 1.29m and mass 2.08kg is pivoted about a horizontal, frictionless pin passing through one end. The rod is released from one end in the vertical position. L y Pivot x At the instant the rod is horizontal, find its angular speed. Submit Answer Tries 0/10 At the instant the rod is horizontal, what is its angluar acceleration? Submit Answer Tries 0/10 At the instant the rod is horizontal, what is the magnitude of its x-component of acceleration at its centre of mass? Submit Answer Tries 0/10 At the instant the rod is horizontal, what is the magnitude of its Y-component of acceleration at its centre of mass? Submit Answer Tries 0/10

Plz asap