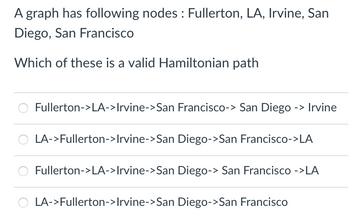
A Hamiltonian path is a concept in graph theory that represents a path in a graph that visits each node (vertex) exactly once. When we encounter a set of nodes and various paths between them, determining a valid Hamiltonian path becomes a puzzle that involves traversing a graph while adhering to certain rules. In the context of the nodes "Fullerton," "LA," "Irvine," "San Diego," and "San Francisco," embark on a journey to discover which sequence constitutes a valid Hamiltonian path. Each step is scrutinized to ensure that no city is revisited and that all cities are visited precisely once. It is a quest for a path that connects these nodes seamlessly, highlighting the essence of Hamiltonian paths in graph theory.
Step by stepSolved in 4 steps

- Mark Zuckerberg, the CEO of Facebook, has hired you to lead the Facebook Algorithms Group. He has asked you to use various graph algorithms to analyze the world's largest social network. The Facebook Graph has 2.8 billion vertices, with each vertex being a Facebook user. Two vertices are connected provided those two users are "friends". The first decision you need to make is how you want to model the Facebook graph. Determine whether you should use an adjacency-list representation or an adjacency-matrix representation.arrow_forward8) Given the following graph and the source node A (the 1st node to be discovered), which of the following could be the 3rd node to be discovered during a BFS?arrow_forwardConsider the following edge-weighted graph with 10 vertices and 17 edges. V-w weight A-B 8. F-A 6. G-B 15 B-F C-B D-C 16 C-G 12 C-H C-I D-I 17 D-E 11 I-E 13 J-E 10 G-F 9. H-G I-H 14 1 I-J Here is a graphical representation of the same edge-weighted graph: (A) -8- (C)------16----- (D)---- --11-----(E) 7|\ 13 10 (F) (G) Give the sequence of edges in the MST in the order that Prim's algorithm adds them to the MST, when starting Prim's algorithm from vertex H. To specify an edge, use its weight.arrow_forward
- A graph has the following edge-endpoint function table. Edge Edgepoints {v. v3} e2 {v2 v3} {v3, Va} {va Vs} e4 {v3, Vs} es {v5, Vs) es ez {vs, V7} eg {v, Vs} eg {v2, v;} Based on the preceding table, find the number of edges incident on the designated vertic Number of edges Vertices incident on the vertex V1 V2 V3 VA V5 V6 V7 V8arrow_forwardPlease send me answer within 10 min!! I will rate you good for sure!!arrow_forwardLook at the attached graph. If the graph, doesn't come up correctly, I have it on GitHub. Github link to graph What is the cost of the optimal path between A and H? F 0.08 E 0.36 0.93 1.09 O 0.68 0.46 O 1.21 0.99 0.27 81 A 0.53 0.1 0.06 G 0.36 0.6E 0.68 0.15 I 0.69 0.29 H 0:33 0.83 0.4, 0.49 B 0.94 Ignore the coloring. I borrowed this image from a discussion post. I can provide a citation after the test. 0.42 D 0.96arrow_forward