Can you please help me solve the attached problem? A solid eylinder rolls down an inclined plane without slipping. The incline makes an angle of 25.0 to thehorizontal, the coefficient of statiec friction is 4, = 0.40, and Igyl = ½MR². Hint - you may not assume thatstatic frietion is at its maximum!(a) Find its acceleration.(b) Find the angle at which static friction is at its maximum, at just above this angle the object will start toslip.

Answered: (a) Find its acceleration. (b) Find the…

Related questions

Question

100%

Can you please help me solve the attached problem?

A solid eylinder rolls down an inclined plane without slipping. The incline makes an angle of 25.0 to the
horizontal, the coefficient of statiec friction is 4, = 0.40, and Igyl = ½MR². Hint - you may not assume that
static frietion is at its maximum!
(a) Find its acceleration.
(b) Find the angle at which static friction is at its maximum, at just above this angle the object will start to
slip.

Expert Solution

Step 1

The Moment of Inertia of a system of particles is the sum of the product of the mass and the square of the distance between the particles and the axis of the rotation. If $m_{1}, m_{2}, m_{3}, . . . ., m_{n}$ are the masses of particles $1, 2, 3, . . ., n$ and $r_{1}, r_{2}, . . . ., r_{n}$ be the distance between them and the axis of rotation. Then the moment of inertia of the system of particles is given by

$I = m_{1} r_{1}^{2} + m_{2} r_{2}^{2} + . . . + m_{n} r_{n}^{2} = \sum_{i = 1}^{n} m_{i} r_{i}^{2}$

Step 2

Let a cylinder of mass M and radius R be rolling down an inclined plane. The external forces acting on the cylinder are the weight of the cylinder in the downward direction, the normal reaction force acting perpendicular to the surface of the inclined plane, and the frictional force acting in the upward and parallel to the inclined plane. The free body diagram of the system is

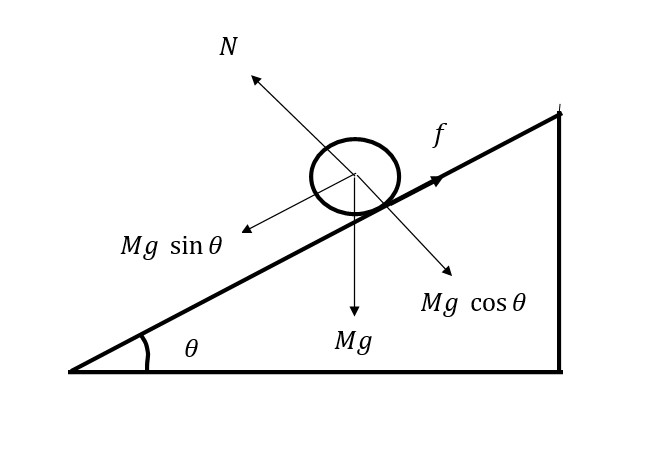
Net force in the downward direction $= M g \sin θ - f$

If $a$ is the linear acceleration of the cylinder then by Newton's second law of motion

$M a = M g \sin θ - f$

Torque due to the frictional force $τ = f R$

Again we know that $τ = I α = \frac{I a}{R}$ where $α$ is the angular acceleration. Then we have

$f R = \frac{I a}{R} \Rightarrow f = \frac{I a}{R^{2}}$

Therefore the force equation is

$M a = M g \sin θ - \frac{I a}{R^{2}} \Rightarrow a = g \sin θ - \frac{I a}{M R^{2}} \Rightarrow a + \frac{I a}{M R^{2}} = g \sin θ \Rightarrow a (1 + \frac{I}{M R^{2}}) = g \sin θ \Rightarrow a = \frac{g \sin θ}{1 + \frac{I}{M R^{2}}}$

Now for a cylinder rolling about an axis passing through the center and perpendicular to its cross-section is

$I = \frac{1}{2} M R^{2}$

a. Therefore the acceleration of the cylinder is

$a = \frac{g \sin θ}{1 + \frac{I}{M R^{2}}} = \frac{g \sin θ}{1 + \frac{\frac{1}{2} M R^{2}}{M R^{2}}} = \frac{g \sin θ}{\frac{3}{2}} = \frac{2}{3} g \sin θ$

For the given problem

$a = \frac{2}{3} g \sin θ = \frac{2}{3} \times 10 \times \sin 25 ° = 2.81 m / s^{2}$

b. The frictional force is given by

$\begin{array}{rcl} f & = & M g \sin θ - M a = M g \sin θ - M (\frac{2}{3} g \sin θ) \\ = & \frac{1}{3} M g \sin θ \end{array}$

The static friction force $f_{s} = μ N$ . Now the normal reaction force is

$N = m g \cos θ$

The condition for rolling without slipping is

$f \leq f_{s}$

This gives

$\frac{1}{3} M g \sin θ \leq μ M g \cos θ \Rightarrow \frac{1}{3} \tan θ \leq μ \Rightarrow μ \geq \frac{1}{3} \tan θ$

The maximum angle at which the body starts slipping can be found using

$μ = \frac{1}{3} \tan θ \Rightarrow θ = \tan^{- 1} (3 μ) = \tan^{- 1} (3 \times 0.4) \Rightarrow θ = 50.19 °$

Step by step

Solved in 3 steps with 1 images

(a) Find its acceleration. (b) Find the angle at which static frietion is at its maximum, at just above this angle the object will start to slip.