
Concept explainers
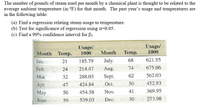
Answer: Regression analysis is concerned with the study of the dependence of one variable, the dependent variable, on one or more other variables, the explanatory variables.
The two - variable linear model, or simple regression analysis, is used for testing hypothesis about the relationship between a dependent variable Y and an independent or explanatory variable X and for prediction. Simple linear regression analysis usually begins by plotting the set of XY values on a scatter diagram and determining by inspection if there exists an approximate linear relationship. It's model is,
Where = intercept or constant and = Slope or coefficient of regressor, e = Error term
In above example Y = The number of pounds of steam usage
X = The average monthly temperature
Fit the regression model Y to X is
Step by stepSolved in 2 steps with 1 images

- Write down the estimated regression equation. What is the value of R square in this regression model? Compared with the R-square in Question 1, what is the additional contribution of gender to the percentage of variance explained? Interpret the meaning of the regression coefficient of Year in College (how does year in college affect salary?). Does this variable have a significant impact on income level at α= .05? How does one more year in college affect salary if the gender is the same? How do you get this conclusion?arrow_forwardA student used multiple regression analysis to study how family spending (y) is influenced by income (x1), family size (x2), and additions to savings (x3). The variables y, x1, and x3 are measured in thousands of dollars. The following results were obtained. ANOVA df SS Regression 3 45.9634 Residual 11 2.6218 Total Coefficients Standard Error Intercept 0.0136 x1 0.7992 0.074 x2 0.2280 0.190 x3 -0.5796 0.920 Write out the estimated regression equation for the relationship between the variables. Compute coefficient of determination. What can you say about the strength of this relationship? Carry out a test to determine whether y is significantly related to the independent variables. Use a 5% level of significant Carry out a test to see if x3 and y are significantly related. Use a 5% level of significance.arrow_forwardA random sample of 102 observations is selected to estimate the relationship between the price of a used car (y) and its odometer readings (x). The estimated simple regression line is: ý = 6533 – 0.03x (0.004) where the value 0.004 in bracket is the standard error of the point estimator for the slope in the regression model. Question 15. What percent of the variability of the used car values can be explained using this model? O 60% O 36% O 80% O 64% O 95% O o o oarrow_forward
- Consider the SPSS regression output below. The dependent variable (Y) is the level of happiness felt by individuals. The dependent variable was measured in the following manner: 1= very unhappy, 2= somewhat unhappy, 3=neither unhappy nor happy, 4= somewhat happy, 5= very happy. The following four factors are the independent variables: highest year of school completed, respondent’s age, number of children of the respondent, and total family income. The researcher acquired data from 1,457 randomly selected Americans and ran a multiple regression. The regression results are presented below: Model Summary Model R R Square Adjusted R Square Std. Error of the Estimate 1 .215a .046 .043 .72476 a. Predictors: (Constant), TOTAL FAMILY INCOME, AGE OF RESPONDENT, NUMBER OF CHILDREN, SUBJECTIVE CLASS IDENTIFICATION, HIGHEST YEAR OF SCHOOL COMPLETED Coefficientsa Model Unstandardized Coefficients Standardized Coefficients t Sig.…arrow_forwardInvestigators want to assess the association between initial serum cholesterol levels (mg/100ml) and presence of coronary artery disease (response), adjusting for age and body mass index (BMI). What is the most appropriate method for assessing this association? 1.Multiple Linear Regression 2.Correlation 3.ANOVA 4.Multiple Logistic Regression 5. Chi-Squared Test Can you tell me why please?arrow_forwardA company has a set of data with employee age (X) and the corresponding number of annual on-the-job-accidents (Y). Analysis on the set finds that the regression equation is Y=60-0.5*X. What can be said of the correspondence (relation) between age and accidents? Are younger workers safer or more prone to accident? What is the likely number of accidents for someone aged 25?arrow_forward
- Weekly sales of a company’s product (y) and those of its main competitor (x) were recorded for one year. Use ?=0.10. a) Conduct a regression analysis of these data. b) Plot the residuals versus the time periods. Does there appear to be autocorrelation? c) Perform the Durbin-Watson test. Is there evidence of autocorrelation? Use ?=0.10 d) If autocorrelation was detected in Part c, propose an alternative regression model to remedy the problem. Use the computer to generate the statistics associated with this model. e) Redo Parts b and c. Compare the two models. PLEASE ONLY USE EXCEL AND SHOW ALL EXCEL COMMANDS! Company Competitor 1383 1153 2022 1067 2429 1296 901 1406 2219 1254 1896 1335 1910 1204 1539 1076 2048 1246 2881 1098 2395 1258 1349 955 2052 954 2675 1363 1588 1022 2704 1155 3148 1807 2822 1295 2217 1116 2260 1323 3040 1326 3137 1107 2977 1163 2599 1254 2412 1017 3187 938 2598 1270 2995 1042 3046 1318 3858 1497…arrow_forwardAs a marketing manager for TriFood, you want to determine whether store Sales (# sold in one month) of TriPower bars are related to price (in cents) of TriPower bars and in-store promotional expenditures (in dollars) for TriPower bars. You conduct a multiple regression analysis with store Sales (Y) as the response variable, and Price (X1) and Promotion (X2) as explanatory variables. Use the pictured Excel regression output below to answer the questions. a) Interpret the value for R square. Interpret the estimated coefficient for price. b) State the hypotheses for assessing the statistical significance of the overall regression equation. Does the model overall fit the data (yes or no?) f) An external consultant to TriFoods believes that for every $1 increase in promotional expenditures, sales will increase by 4.7 units. Test the consultant's hypothesis at a 5% significance level using both approaches (tcalc vs tcrit and p-value vs a).arrow_forwardRetail price data for n = 60 hard disk drives were recently reported in a computer magazine. Three variables were recorded for each hard disk drive: y = Retail PRICE (measured in dollars) X1 = Microprocessor SPEED (measured in megahertz) (Values in sample range from 10 to 40) x 2 = CHIP size (measured in computer processing units) (Values in sample range from 286 to 486) A first-order regression model. was fit to the data. Part of the printout follows: Parameter Estimates T FOR 0 ERROR PARAMETER = 0 PROB>ITI PARAMETER STANDARD VARIABLE DF ESTIMATE INTERCEPT 1 -373.526392 1258.1243396 -0.297 0.7676 SPEED 1 104.838940 22.36298195 4 688 0.0001 сHP 1 3.571850 3.89422935 0.917 0.3629 Identify and interpret the estimate of B2-arrow_forward
- Ten observations were provided for a dependent variable y and two independent variables x₁ and x₂; for these data, SST = 15,185.9 and SSR = 14,053.3. (a) Compute R². (Round your answer to three decimal places.) R² = (b) Compute R. (Round your answer to three decimal places.) Ka (c) Does the estimated regression equation explain a large amount of the variability in the data? Explain. (For purposes of this exercise, consider an amount large if it is at least 55%. Round your answer to one decimal place.) ---Select--- V , after adjusting for the number of independent variables in the model, we see that % of the variability in y has been accounted for. Need Help? Read It Watch Itarrow_forwardA multiple regression model was fit to predict domestic gross for movies based off of the production budget, opening weekend gross and number of stars. The overall F test p-value equals 0.252. What conclusion can you make at alpha = 0.05? All of the variables contribute to the model. At least one of the variables contributes to the model. O None of the variables contribute to the model.arrow_forwardThe quality of the orange juice produced by a manufacturer is constantly monitored. There are numerous sensory and chemical components that combine to make the best-tasting orange juice. For example, one manufacturer has developed a quantitative index of the "sweetness" of orange juice. Suppose a manufacturer wants to use simple linear regression to predict the sweetness (y) from the amount of pectin (x). Find a 90% confidence interval for the true slope of the line. Interpret the result. Click the icon to view the data collected on these two variables during 24 production runs at a juice-manufacturing plant. A 90% confidence interval for the true slope of the line is (☐.). (Round to four decimal places as needed.) Data table Run Sweetness Index Pectin (ppm) 1 5.2 220 2 5.5 226 3 6.0 259 4 5.9 210 5 5.8 224 6 6.0 215 7 5.8 232 8 5.6 266 9 5.6 239 10 5.9 212 11 5.4 410 12 5.6 255 13 5.7 304 14 5.5 259 15 5.3 284 16 5.3 383 17 5.6 271 18 5.5 264 19 5.7 226 NNNNN 20 5.3 263 21 5.9 232 22…arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





