Question
Please show all work and answer all parts

Transcribed Image Text:**Title: Understanding Tension and Motion in a Pulley System**
**Introduction:**
This problem involves a two-block system connected by a rope over a pulley, a classic physics scenario used to illustrate concepts of tension, force, and acceleration.
**Problem Statement:**
A light rope is attached to a block \( m_1 = 6.00 \, \text{kg} \) that rests on a frictionless, horizontal surface. The rope passes over a frictionless, massless pulley, and a block with mass \( m_2 \) is suspended from the other end. When the blocks are released, the tension in the rope is \( 17.0 \, \text{N} \).
**Diagram Explanation:**
- The diagram shows a horizontal surface with block \( m_1 \) on it. The rope is connected to block \( m_1 \), passes over a pulley, and is attached to block \( m_2 \) which is hanging vertically.
**Questions:**
**(a) Draw two free-body diagrams: one for each block.**
- **Block \( m_1 \):** Draw forces including the tension \( T \) from the rope acting horizontally, and the normal force and gravitational force acting vertically.
- **Block \( m_2 \):** Draw the gravitational force \( m_2 \cdot g \) acting downward and the tension \( T \) from the rope acting upward.
**(b) What is the acceleration of either block?**
- Here, use Newton’s second law \( F = m \cdot a \) to find the acceleration considering the forces and given tension.
**(c) Find \( m_2 \).**
- Apply the equations of motion to solve for the unknown mass \( m_2 \) using the given tension and calculated acceleration.
**(d) How does the tension compare to the weight of the hanging block? Why?**
- Discuss the relationship between tension in the rope and the gravitational force on \( m_2 \). Note that tension will differ from weight due to the system's acceleration.
By solving this problem, students will deepen their understanding of dynamics and the interplay of forces in a system involving pulleys.
Expert Solution
arrow_forward
Step 1
a)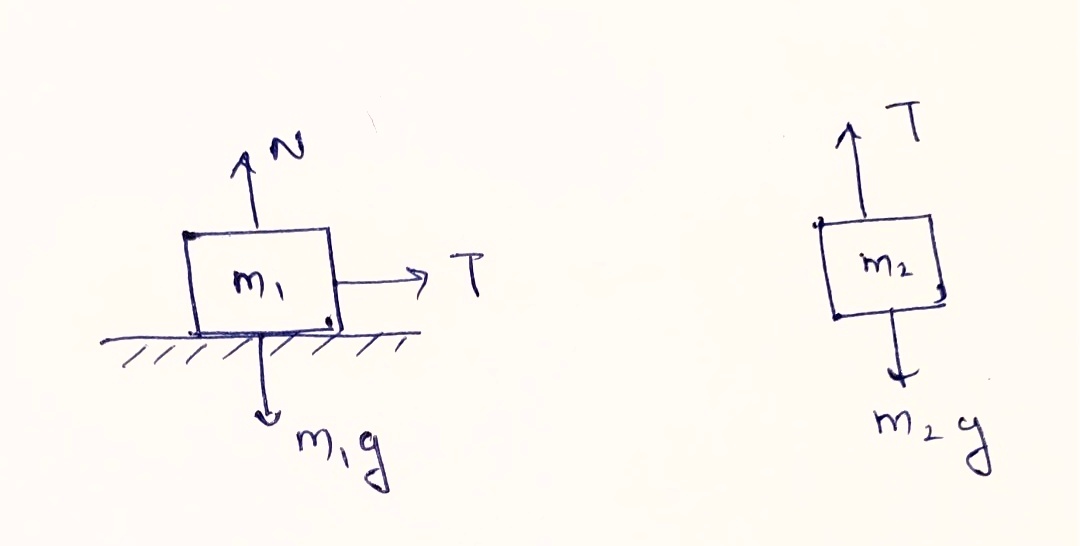
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios