Related questions
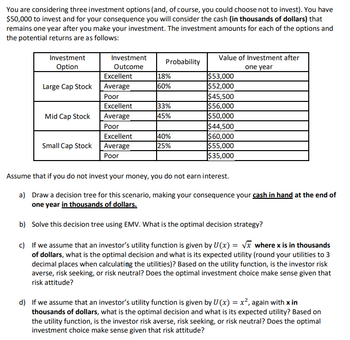
You are considering three investment options (and, of course, you could choose not to invest). You have
$50,000 to invest and for your consequence you will consider the cash (in thousands of dollars) that
remains one year after you make your investment. The investment amounts for each of the options and
the potential returns are as follows: Investment
Option
Investment
Outcome Probability Value of Investment after
one year
Large Cap Stock
Excellent 18% $53,000
Average 60% $52,000
Poor $45,500
Mid Cap Stock
Excellent 33% $56,000
Average 45% $50,000
Poor $44,500
Small Cap Stock
Excellent 40% $60,000
Average 25% $55,000
Poor $35,000
Assume that if you do not invest your money, you do not earn interest.
a) Draw a decision tree for this scenario, making your consequence your cash in hand at the end of
one year in thousands of dollars.
b) Solve this decision tree using EMV. What is the optimal decision strategy?
c) If we assume that an investor’s utility
of dollars, what is the optimal decision and what is its expected utility (round your utilities to 3
decimal places when calculating the utilities)? Based on the utility function, is the investor risk
averse, risk seeking, or risk neutral? Does the optimal investment choice make sense given that
risk attitude?
d) If we assume that an investor’s utility function is given by ?(?) = ?
2
, again with x in
thousands of dollars, what is the optimal decision and what is its expected utility? Based on
the utility function, is the investor risk averse, risk seeking, or risk neutral? Does the optimal
investment choice make sense given that risk attitude?
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 1 images
- Please answer. I'll give rate. Thanksarrow_forwardRichies insurance company offers a 250,000 life insurance policy for a premium of $750 per year. If the probability you live through the year is .9977 what is the expected value to the insurance companyarrow_forwardPlease do question 1f and 1g handwrittenarrow_forward
- C. Determine how much the firm would be willing to pay to a market research firm to gain better information about future market conditions. 10. An investor must decide between two altemative investments-stocks and bonds. The return for each investment, given two future economic conditions, is shown in the following payoff table: Economic Conditions Investment Good Bad Stocks S10,000 S-4.000 Bonds 7.000 2,000 What probability for each economic condition would make the investor indifferent to the choice between stocks and bonds? 11.In Problem 5, Ann Tyler, with the help of a financial newsletter and some library research, has been able to assign probabilities to each of the possible interest rates during the next year, as follows:arrow_forwardYou own a fruit garden. Choose one of the followings by showing clear calculation. Yearly inflation rate is 5%. Option A: Invest 3 lac BDT to buy cultivation tools/factory. At end of every year you may gain high (8 lac BDT), medium (3 lac BDT) or low (1 lac BDT) with respective probability 0.3, 0.4 and 0.3 for the next 5 years. Option B: Lease the garden. The lessee pays 3.5 lac BDT at the beginning of each year for the next 5 years. There is risk of plant mortality due to hyper production. Loss may be high: 9 lac BDT (probability 0.1) or low: 1 lac BDT. This loss is realized at the end of 5th year only.arrow_forwardTyson Corp. stock has returns of 3%, 18%, -24%, and 28% for the past four years. Based on this information, what is the 99% probability range for any one given year? Select one: Oa 24.5 to 34.3% O b.-61.7 to 74.2% OC.-8.4 to 11.7% Od.-16.4 to 28.9% e. 39.0 to 51.5%arrow_forward
- ogle.com/d/1NGOHXPHTvH8PLnxmRZFacGXUv00o4rY1EStn8YtOx41/viewer?f%=3 ch Media services/El.. EWhat's Going On in... G Bases housing U.S.. Digital Passport by.. hment 2 - 1.3 + 1.4 419 ackground Clear frame 1.3 2) How many 4 letter permutations can be formed from the letters in word rhombus? 3) A board of directors composed of eight people must select board officers. In how man president, vice president, and treasurer be selected from this 8-person board?arrow_forwardThe probability that a 80-year-old female in the U.S. will die within one year is about 0.048711. An insurance company is preparing to sell a 80-year-old female a one-year, $20,000 life insurance policy. How much should it charge for its premium in order to have a positive expectation for the policy? (Round your answer to the nearest dollar.)$arrow_forward
- A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
