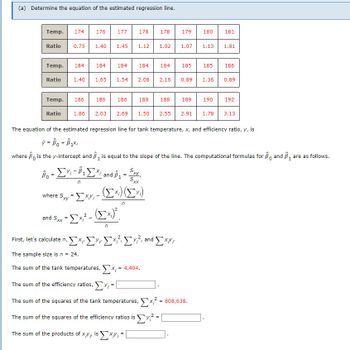
(a) Determine the equation of the estimated regression line. Temp. Ratio 174 176 177 0.75 1.40 1.45 Temp. 184 184 Ratio 1.40 1.65 1.54 Temp. 186 186 Ratio 184 186 178 178 1.12 184 184 2.08 2.16 188 1.02 βο - Σν-βι Σ× and β, - Sm 1 = 5xx Π S. where sx = Σ× - (Σ») (Σ») Π and Sxx => Π First, let's calculate n, Σ× ΣΥΣ? ΣΥ? and Σ ΣΣΣΣΥ, The sample size is n = 24. The sum of the tank temperatures, Σ×, = 4,404. The sum of the efficiency ratios, ΣΥ; = 188 179 180 1.07 1.13 1.81 0.89 185 185 186 189 181 1.86 2.03 2.69 1.50 2.55 2.91 1.78 3.13 The equation of the estimated regression line for tank temperature, x, and efficiency ratio, y, is P-Bot Box, where β o is the y-intercept and Î, is equal to the slope of the line. The computational formulas for ßo and β, are as follows. 1.36 0.89 190 192

A sample of 4000 bacteria triples every 7 hours. How many bacteria are left after 10 hours. Round to nearest integer.

Please number 4.

Part c looks incomplete. Can it be reviewed please.

2. If 4 times a number is added to 5, the result is 35 more than the number. Find the number.