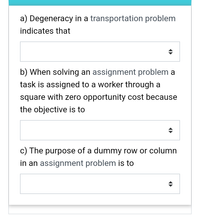
a) Degeneracy in a transportation problem indicates that b) When solving an assignment problem a task is assigned to a worker through a square with zero opportunity cost because the objective is to c) The purpose of a dummy row or column in an assignment problem is to

8 The Hatfields, Montagues, McCoys, and Capulets are going on their annual family picnic. Four cars are available to transport the families to the picnic. The cars can carry the following number of people: car 1, four; car 2, three; car 3, three; and car 4, four. There are four people in each family, and no car can carry more than two people from any one family. Formulate the problem of transporting the maximum possible number of people to the picnic as a maximum-flow problem.

26. Scheduling Five different charity organizations send trucks on various routes to pick up donations that residents leave on their doorsteps. Charity A covers Main St., First Ave., and State St. Charity B covers First Ave., Second Ave., and Third Ave. Charity C covers State t., City Dr., and Country Lane. Charity D covers City Dr., Second Ave., and Main St. Charity E covers Third Ave., Country Lane, and Fourth Ave. Each charity has its truck travel down all three streets on its route on the same day, but no two charities wish to visit the same streets on the same day. Use graph coloring to design a schedule for the charities. Arrange their pickup routes so that no street is visited twice on the same day by different charities. The schedule should use the least possible number of days.