MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Question
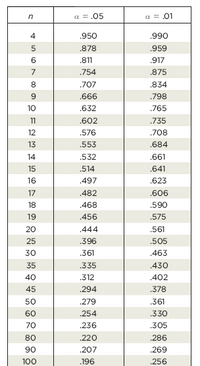
Transcribed Image Text:Certainly! Here is a transcription of the table from the image, which is suitable for an educational website:
---
**Table of Critical Values for Correlation Coefficients**
This table presents critical values for testing the significance of correlation coefficients at two significance levels (\(\alpha = 0.05\) and \(\alpha = 0.01\)). These values indicate the threshold above which a correlation coefficient is considered statistically significant for a given sample size (\(n\)).
| \(n\) | \(\alpha = 0.05\) | \(\alpha = 0.01\) |
|-------|-----------------|-----------------|
| 4 | 0.950 | 0.990 |
| 5 | 0.878 | 0.959 |
| 6 | 0.811 | 0.917 |
| 7 | 0.754 | 0.875 |
| 8 | 0.707 | 0.834 |
| 9 | 0.666 | 0.798 |
| 10 | 0.632 | 0.765 |
| 11 | 0.602 | 0.735 |
| 12 | 0.576 | 0.708 |
| 13 | 0.553 | 0.684 |
| 14 | 0.532 | 0.661 |
| 15 | 0.514 | 0.641 |
| 16 | 0.497 | 0.623 |
| 17 | 0.482 | 0.606 |
| 18 | 0.468 | 0.590 |
| 19 | 0.456 | 0.575 |
| 20 | 0.444 | 0.561 |
| 25 | 0.396 | 0.505 |
| 30 | 0.361 | 0.463 |
| 35 | 0.335 | 0.430 |
| 40 | 0.312 | 0.402 |
| 45 | 0.294
![**Title: Evaluating Linear Correlation Between Weights of Discarded Paper and Glass**
**Introduction:**
A data set includes weights of garbage discarded in one week from 62 different households. The paired weights of paper and glass were used to obtain the results shown. Is there sufficient evidence to support the claim that there is a linear correlation between weights of discarded paper and glass? Use a significance level of α = 0.05.
**Data Table:**
- **Correlation matrix:**
| Variables | Paper | Glass |
|-----------|--------|---------|
| Paper | 1 | 0.1666 |
| Glass | 0.1666 | 1 |
**Hypotheses:**
- **Null Hypothesis (H₀):** ρ = 0
- **Alternative Hypothesis (H₁):** ρ ≠ 0
**Statistical Analysis:**
1. **Identify the test statistic, r:**
- r = [Input field]
- (Round to three decimal places as needed.)
2. **Identify the critical value(s):**
- (Round to three decimal places as needed.)
- Options:
- A. There is one critical value at r = [Input field]
- B. There are two critical values at r = ±[Input field]
**Conclusion:**
State the conclusion based on the test statistic and critical value:
- Because the absolute value of the test statistic is [Input field] the positive critical value, there [Dropdown: "is"/"is not"] sufficient evidence to support the claim that there is a linear correlation between the weights of discarded paper and glass for a significance level of α = 0.05.
This exercise helps understand the process of testing for linear correlation between two variables using correlation coefficients and critical values.](https://content.bartleby.com/qna-images/question/e2e363c5-2472-4cf7-839e-3830821f17e5/9e4dcc20-3ebb-45b5-86a9-6db6cc9b3988/2qkp67e_processed.png)
Transcribed Image Text:**Title: Evaluating Linear Correlation Between Weights of Discarded Paper and Glass**
**Introduction:**
A data set includes weights of garbage discarded in one week from 62 different households. The paired weights of paper and glass were used to obtain the results shown. Is there sufficient evidence to support the claim that there is a linear correlation between weights of discarded paper and glass? Use a significance level of α = 0.05.
**Data Table:**
- **Correlation matrix:**
| Variables | Paper | Glass |
|-----------|--------|---------|
| Paper | 1 | 0.1666 |
| Glass | 0.1666 | 1 |
**Hypotheses:**
- **Null Hypothesis (H₀):** ρ = 0
- **Alternative Hypothesis (H₁):** ρ ≠ 0
**Statistical Analysis:**
1. **Identify the test statistic, r:**
- r = [Input field]
- (Round to three decimal places as needed.)
2. **Identify the critical value(s):**
- (Round to three decimal places as needed.)
- Options:
- A. There is one critical value at r = [Input field]
- B. There are two critical values at r = ±[Input field]
**Conclusion:**
State the conclusion based on the test statistic and critical value:
- Because the absolute value of the test statistic is [Input field] the positive critical value, there [Dropdown: "is"/"is not"] sufficient evidence to support the claim that there is a linear correlation between the weights of discarded paper and glass for a significance level of α = 0.05.
This exercise helps understand the process of testing for linear correlation between two variables using correlation coefficients and critical values.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Police sometimes measure shoe prints at crime scenes so that they can learn something about criminals. Listed below are shoe print lengths, foot lengths, and heights of males. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Based on these results, does it appear that police can use a shoe print length to estimate the height of a male? Use a significance level of a=0.05. Shoe Print (cm) 28.8 28.8. 32.1 32.6 Foot Length (cm) Height (cm) 25.2 181.7 24.9 173.5 27.5 27.6 27.5 25.9 186 169.1 171 Construct a scatterplot. Choose the correct graph below. OA. 200- 2 160+ Shoe Print (cm) 35 The linear correlation coefficient is r= (Round to three decimal places as needed.) B. 200- 160- 25 Shoe Print (cm) ○ C. 200- G 35 160+ 25 Shoe Print (cm) 35 OD. Q 200- Height (cm) G 160- 25 35 Shoe Print (cm)arrow_forwardListed below are paired data consisting of amounts spent on advertising (in millions of dollars) and the profits (in millions of dollars). Determine if there is a significant linear correlation between advertising cost and profit . Use a significance level of 0.05 and round all values to 4 decimal places. Advertising Cost Profit 3 19 4 16 24 6 29 7 25 27 10 30 Ho: p = 0 На: р * 0 Find the Linear Correlation Coefficient r = Find the p-value p-value = The p-value is O Less than (or equal to) a O Greater than a The p-value leads to a decision to O Do Not Reject Ho O Accept Ho O Reject Ho The conclusion is O There is a significant negative linear correlation between advertising expense and profit. O There is a significant linear correlation between advertising expense and profit. O There is a significant positive linear correlation between advertising expense and profit. O There is insufficient evidence to make a conclusion about the linear correlation between advertising expense and…arrow_forwardThe table below includes data from taxi rides. The distances are in miles, the times are in minutes, the fares are in dollars, and the tips are in dollars. Is there sufficient evidence to conclude that there is a linear correlation between the time of the ride and the tip amount? Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Use a significance level of a = 0.01. Does it appear that riders base their tips on the time of the ride? Click here for information on the taxi rides. Construct a scatterplot. Choose the correct graph below. O A. Tip Amount ($) 25- Q 0 35 G Ride time (minutes) Determine the linear correlation coefficient. The linear correlation coefficient is r= (Round to three decimal places as needed.) Tip Amount ($) B. 25- 0- 0 35 G Ride time (minutes) Taxi data ip Amount (S C. 25- 0- 35 Ride time…arrow_forward
- Police sometimes measure shoe prints at crime scenes so that they can learn something about criminals. Listed below are shoe print lengths, foot lengths, and heights of males. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Based on these results, does it appear that police can use a shoe print length to estimate the height of a male? Use a significance level of a= 0.01. Shoe Print (cm) | 28.8 Foot Length (cm) 24.8 Height (cm) 30.8 30.4 31.1 28.6 24.6 27.8 26.1 25.3 177.6 179.2 179.2 169.4 169.5arrow_forwardPolice sometimes measure shoe prints at crime scenes so that they can learn something about criminals. Listed below are shoe print lengths, foot lengths, and heights of males. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Based on these results, does it appear that police can use a shoe print length to estimate the height of a male? Use a significance level of a = 0.05. Shoe Print (cm) Foot Length (cm) Height (cm) Height (cm) 160- 25 Shoe Print (cm) 30.1 25.7 179 35 0 30.1 32.4 32.8 25.1 27.5 27.1 176.9 187.3 170.8 The linear correlation coefficient is r= 0.495 (Round to three decimal places as needed.) Determine the null and alternative hypotheses. Ho: p = H₁: P 0 (Type integers or decimals. Do not round.) The test statistic is t = 0.99. (Round to two decimal places as needed.) The P-value is (Round to three…arrow_forwardFor which of these research situations would you most likely calculate a Pearson's r correlation coefficient? independent variable = age; dependent variable = memory test score independent variable = type of car owned; dependent variable = money spent on gasoline per week independent variable = college major; dependent variable = GPA independent variable = city of residence; dependent variable = miles driven per weekarrow_forward
- Fifty-four wild bears were anesthetized, and then their weights and chest sizes were measured and listed in a data set. Results are shown in the accompanying display. Is there sufficient evidence to support Correlation Results the claim that there is a linear correlation between the weights of bears and their chest sizes? When measuring an anesthetized bear, is it easier to measure chest size than weight? If so, does it appear that Correlation coeff, r: 0.959614 a measured chest size can be used to predict the weight? Use a significance level of = 0.05. Critical r: +0.2680855 P-value (two tailed): 0.000 Но: Р H1:P (Type integers or decimals. Do not round.) Identify the correlation coefficient, r. (Round to three decimal places as needed.) Identify the critical value(s). (Round to three decimal places as needed.) O A. There is one critical value at r= . B. There are two critical values at r= ± Is there sufficient evidence to support the claim that there is a linear correlation between…arrow_forwardThe accompanying table lists the ages of acting award winners matched by the years in which the awards were won. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Should we expect that there would be a correlation? Use a significance level of a=0.05. Click the icon to view the ages of the award winners. Construct a scatterplot. Choose the correct graph below. A. 20- 20 E 70 OB. 70- 20+ 20 70 Best Actress (years) The linear correlation coefficient is r= (Round to three decimal places as nee Best Actress (years) Best Actresses and Best Actors Best Actress 28 31 30 64 31 Best Actor 44 39 37 43 49 33 46 47 56 OC. COD. Q 70- 20 20 Best Actress (years) 30 59 23 42 53 442 52 39 56 44 34 70 20 20 70 Best Actress (years)arrow_forwardThe accompanying table lists the ages of acting award winners matched by the years in which the awards were won. Construct a scatterplot, find the value of the linear correlation coefficient r, and find the P-value of r. Determine whether there is sufficient evidence to support a claim of linear correlation between the two variables. Should we expect that there would be a correlation? Use a significance level of a = 0.01. Click the icon to view the ages of the award winners. Construct a scatterplot. Choose the correct graph below. OA. 70- Best Actor (years) 20+ 20 Q [ 70 Best Actress (years) The linear correlation coefficient is r= ☐ (Round to three decimal places as needed.). B. OC. Q 70- 70- Q 20- 20 20- 70 20 70 Best Actress (years) Best Actress (years) Best Actresses and Best Actors Best Actress 29 29 28 57 31 32 45 28 63 22 42 51D Best Actor 45 39 39 47 51 49 64 48 38 55 43 34 O D. 70- Q G 20 20 70 Best Actress (years)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman