Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
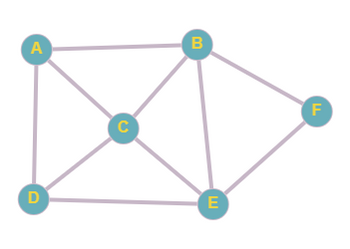
- In your own words, explain what is required for a trail or circuit to be a Euler trail or circuit.
- Does a Euler trail exist for their graph? Explain specifically using the label and degree of each vertex.
- Does a Euler circuit exist for their graph? Explain specifically using the label and degree of each vertex.
There are 6 people that discussing their favorite foods. Each person will be represented with a letter. A, B, C, D, E, F. Person A, B, and C really like Ice cream. Person D really likes cookies. Person A and C agree that cookies are good. Person D, C, and E like soup quite a bit, and person C, B, and E really like salad. Person B, E, and F all agree that cake is good too. So, person A really likes ice cream and cookies. Person B really likes ice cream, salad, and cake. Person C really likes ice cream, cookies, soup, and salad. Person D really likes cookies and soup. Person E really likes salad and cake. Person F only likes cake. The below graph represents this relationship. Each vertex represents a person, and every edge represents their relationship in similar food preferences to each other. Even if two people share more than one food preference, there will only be one edge connecting them as the edge is just representing that they both like at least one similar food.
Transcribed Image Text:A
D
B
E
F
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps
Knowledge Booster
Similar questions
- Draw the graph of four-dimensional cube. How many edges and vertices arethere?arrow_forwardDraw a graph with six vertices and two bridges. A. OB. Oc. OD. acerarrow_forwardGraphs 1. Describe each graph below. Explain how many vertices and how many edges it has, and if it is a tree or not a tree. 1 10 C Write your response below:arrow_forward
- Draw a graph that models the connecting relationships in the floorplan below. The vertices represent the rooms and the edges represent doorways connecting the rooms. Vertex F represents the outdoors. F ㅓㅏ A B T E Is it possible to find a circuit through the house that uses each doorway once? If so, enter the sequence of rooms (vertices) visited, for example ABDEA. If it is not possible, enter DNE.arrow_forwardThe diagram on the right is a floor plan. Letting vertices represent the room and the outside, and edges represent the connecting doors, which graph correctly models the floor plan? O A D B rwin =yes A I HH D C ㅓㅏ B 11arrow_forwardRead all directions before answering a question. This assignment is conceptual in nature so no work is needed BUT be sure to be clear and state all answers in complete sentences where needed. Write answers on this sheet. 1) Determine how many vertices and edges the graph has and the degree of each vertex. State the degree next to the vertex OR state the vertex label letter and the degree in the space to the right of the graph. A B E с D # of vertices = # of edges =arrow_forward
- 1) Definitions. The graph below shows 5 cities. The weights on the edges represent the airfare for a one-way flight between the cities. a. How many vertices and edges does the graph have? b. Is the graph connected? c. What is the degree of the vertex representing LA? d. If you fly from Seattle to Dallas to Atlanta, is that a path or a circuit? And what is its cost? e. If you fly from LA to Chicago to Dallas to LA, is that a path or a circuit? And what is its cost? f. Is the graph a complete graph? If so, how many Hamiltonian circuits does it have? Seattle LA $100 $70 $150- $145 Chicago $170 $75 $120 $140 $165 $85 Atlanta Dallasarrow_forwardDraw a graph that models the connecting relationships in the floorplan below. The vertices represent the rooms and the edges represent doorways connecting the rooms. Vertex F represents the outdoors. F B E Is it possible to find a circuit through the house that uses each doorway once? If so, enter the sequence of rooms(vertices) visited, for example ABDEA. If it is not possible, enter DNE.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,