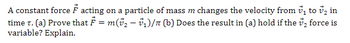
A constant force Facting on a particle of mass m changes the velocity from ₁ to ₂ in time T. (a) Prove that ♬ = m(v₂ − ₁)/π (b) Does the result in (a) hold if the v₂ force is variable? Explain.

Find the velocity (in m/s) of a proton that has a momentum of 3.88 ✕ 10−19 kg · m/s.

There are two relativistic particles of identical mass m that move towards each other along the same axis. The magnitudes of their momenta are the same. They collide head-on to form a new particle of mass 8m. What were the magnitudes of momenta of the initial particles?

Suppose two particles are traveling along the space curves r1(t)=< t2,, 8t-16, t2 > and r1(t)=< 3t+4, t2, 5t-4, >.  A collision will occur when the two particles arrive at the same point at the same time.  Find any time(s) and location(s) when and where the particles collide

k A 13.00 kg particle starts from the origin at time zero. Its velocity as a function of time is given by = 10t² + 1tj where is in meters per second and t is in seconds. (Use the following as necessary: t.) V (a) Find its position as a function of time. ŕ= esc 10/³1 + ²/2 2²; 3 (b) Describe its motion qualitatively. The particle starts from rest at the origin, starts moving in the y direction, and gains speed faster and faster while turning to move more and more nearly parallel to the x axis. Score: 0.06 out of 0.06 Comment: (c) Find its acceleration as a function of time. a = 20ti + lj m/s² (d) Find the net force exerted on the particle as a function of time. F= T= (e) Find the net torque about the origin exerted on the particle as a function of time. N m X X (f) Find the angular momentum of the particle as a function of time. Ľ Need Help? Read It F1 N x (g) Find the kinetic energy of the particle as a function of time. K= x kg m²/s X (h) Find the power injected into the particle as a…

We track the particle’s trajectory between t = 0 to t = T. During this interval, how much time transpires in the particle’s non-inertial reference frame?

4. A rocket accelerates by burning its onboard fuel, so that its mass decreases with time.Suppose that the initial mass of the rocket at liftoff (including its fuel) is m, the fuel isconsumed at rate r, and the exhaust gases are ejected with constant velocity ν (relativeto the rocket). A model for the velocity of the rocket at time t is given by the equationv(t) = −ν ln(1 −Rt) −gt,where g is the acceleration due to gravity, R = r/m, and t is not too large.(a) Find an expression for the acceleration, a(t) = v′(t), of the rocket at any time t.(b) Find an expression for the position of the height, h(t), of the rocket at any timet. You can assume that at t = 0, the rocket hasn’t left the ground. Hint: re-member that ν,R,g are all constants and t is the independent variable.Write out your steps carefully!(c) Let g = 9.8 m/s2, R = 0.005 s−1. What does the velocity of the exhaust gases,ν, need to be for the rocket to reach a height of 6000 m one minute after liftoff?You can round to the…

(b) A particle of unit mass moving in one dimension obeys the equation of motion x = (i) Show that i2 – e" is a constant of the motion. (ii) At t = 0 the particle is at x = 0 and at rest, i.e. x(0) = ¿(0) = 0. Show that the particle reaches x = +o at finite t > 0. Hint: use the result of part (i) to write the time taken to reach x = +0 as an integral. (iii) What is a suitable Lagrangian for this system?

A particle of mass M, which was initially at rest, is hit by a particle of mass m, which is travelling at the speed Vi. The two particles collide and travel in different directions at the same pace Vf. Find the mass ratio M/m in terms of ß = vi/c, assuming a relativistic, elastic collision. Demonstrate that this reduces to Vi 0, the nonrelativistic meaning.