
A company wishes to produce two types of souvenirs: Type A and Type B. Each Type A souvenir will result in a profit of $1, and each Type B souvenir will result in a profit of $1.20. To manufacture a Type A souvenir requires 2 minutes on Machine I and 1 minute on Machine II. A Type B souvenir requires 1 minute on Machine I and 3 minutes on Machine II. There are 3 hours available on Machine I and 5 hours available on Machine II.
(b) Find the contribution to the profit of a Type A souvenir (with the contribution to the profit of a Type B souvenir held at $1.20), given that the optimal profit of the company will be $208.80.
$
(c) What will be the optimal profit of the company if the contribution to the profit of a Type B souvenir is $2.00 (with the contribution to the profit of a Type A souvenir held at $1.00)?
$
Let x is number of Type A souveners produced and y is number of Type B souveners produced.
Then total profit is given by the profit function P(x,y) = x+1.2y
This becomes our objective function which is to be maximized.
Now we restrict x and y to the given inequalities.
Total time taken on machine A = 2x+y 3
60 = 180 mins
2x+y
180
Total time taken on machine B = x+3y 5
60 = 300 mins
x+3y
300
Also x,y 0
The first two inequalities will be towards the side containing origin
Plotting these inequalities on graph, we will get optimal solution to the profit equation
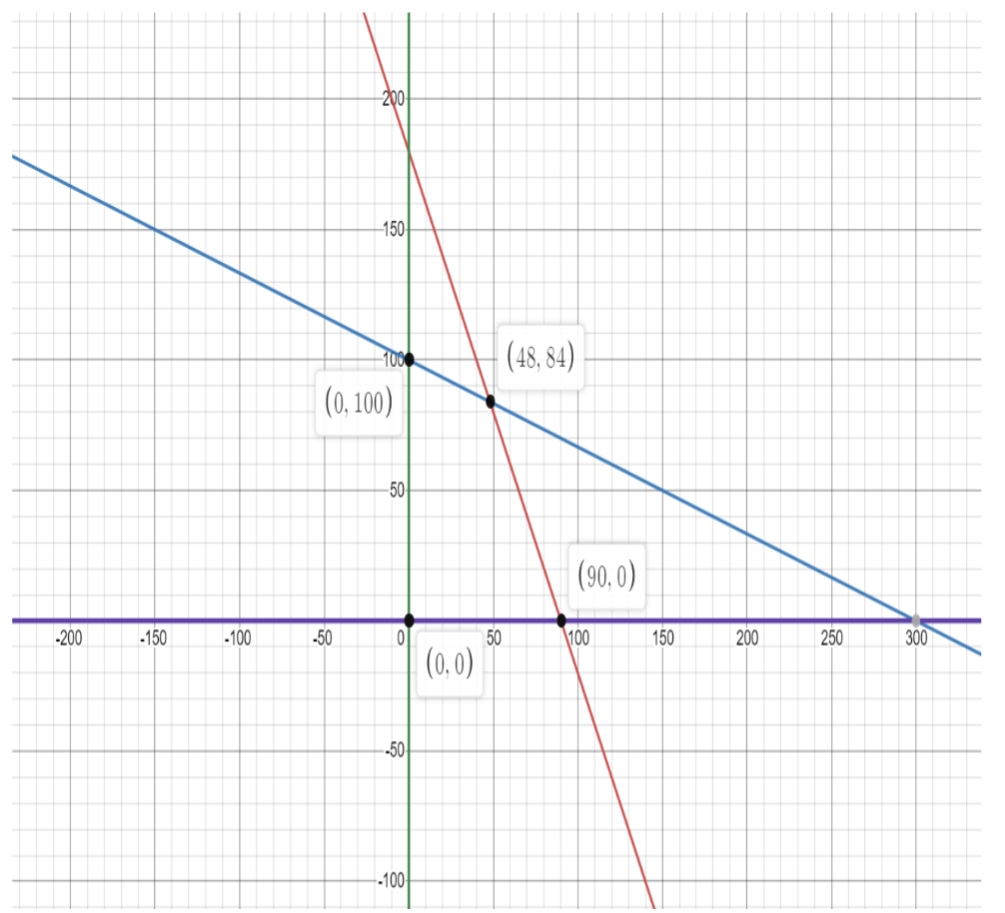
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 13 images

- A company wishes to produce two types of souvenirs: Type A and Type B. Each Type A souvenir will result in a profit of $1, and each Type B souvenir will result in a profit of $1.20. To manufacture a Type souvenir requires 2 minutes on Machine I and 1 minute on Machine II. A Type B souvenir requires 1 minute on Machine I and 3 minutes on Machine II. There are 3 hours available on Machine I and 5 hours available on Machine II. (a) The optimal solution holds if the contribution to the profit of a Type B souvenir lies between $ THER and $ (Enter your answers from smallest to largest.) (b) Find the contribution to the profit of a Type A souvenir (with the contribution to the profit of a Type B souvenir held at $1.20), given that the optimal profit of the company will be $208.80. $ (c) What will be the optimal profit of the company if the contribution to the profit of a Type B souvenir is $3.00 (with the contribution to the profit of a Type A souvenir held at $1.00)? $arrow_forwarderth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $15,000/day to operate, and it yields 65 oz of gold and 2900 oz of silver each day. The Horseshoe Mine costs $15,500/day to operate, and it yields 70 oz of gold and 1300 oz of silver each day. Company management has set a target of at least 540 oz of gold and 16,800 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost? Saddle- Days Horseshoe- Days Minimum Cost-arrow_forwardA carpenter builds bookshelves and tables for a living. Each bookshelf takes one box of screws, two 2 ✕ 4's, and three sheets of plywood to make. Each table takes two boxes of screws, two 2 ✕ 4's, and four sheets of plywood. The carpenter has 55 boxes of screws, 70 2 ✕ 4's, and 115 sheets of plywood on hand. In order to maximize their profit using these materials on hand, the carpenter has determined that they must build 10 shelves and 20 tables. How many of each of the materials (boxes of screws, 2 ✕ 4's, and sheets of plywood) are leftover, when the carpenter builds 10 shelves and 20 tables? The carpenter has _ boxes of screws, _ 2 ✕ 4's, and _ sheets of plywood leftover.arrow_forward
- A farmer has 165 acres of land suitable for cultivating crops A and B. He has enough seeds available to plant 110 acres of crop A and 115 acres of crop B. Each acre of crop A requires 18 hours of labor, and each acre of crop B requires 19 hours of labor. The farmer has at most 3420 hours of labor available. He expects to make a profit of 130 dollars per acre on crop A and 190 dollars per acre on crop B. How many acres should the farmer plant in order to maximize his profit? acres of crop A, and acres of crop B.arrow_forwardPham can work as many or as few hours as she wants at the college bookstore for $9 per hour. But due to her hectic schedule, she has just 15 hours per week that she can spend working at either the bookstore or other potential jobs. One potential job, at a café, will pay her $12 per hour for up to 6 hours per week. She has another job offer at a garage that will pay her $10 an hour for up to 5 hours per week. And she has a potential job at a daycare center that will pay her $8.50 per hour for as many hours as she can work. If her goal is to maximize the amount of money she can make each week, how many hours will she work at the bookstore?arrow_forwardA toy factory creates miniature steel train engines and box cars. The fabrication department has 3,679 minutes available per week and the assembly and finishing department has 3,099 minutes available per week. Manufacturing one miniature steel train engine requires 8 minutes of fabrication and 5 minutes of assembling and finishing. Manufacturing one miniature steel box car requires 4 minutes of fabrication and 5 minutes of assembling and finishing. The profit on each miniature steel train engine is $8.00 and the profit on each miniature steel box car is $7.25. How many steel train engines and steel box cars should be produced each week to obtain the maximum profit? Find the maximum weekly profit. (Use x for box car and y for train engine.) Maximize P subject to %3D < 3, 679 < 3, 099 Enter the solution to the simplex matrix below. If there is no solution enter 'DNE' in the boxes below. If more than one solution exists, enter only one of the multiple solutions below. If needed round toys…arrow_forward
- A company wishes to produce two types of souvenirs: Type A and Type B. Each Type A souvenir will result in a profit of $1, and each Type B souvenir will result in a profit of $1.20. To manufacture a Type A souvenir requires 2 minutes on Machine I and 1 minute on Machine II. A Type B souvenir requires 1 minute on Machine I and 3 minutes on Machine II. There are 3 hours available on Machine I and 5 hours available on Machine II. (a) The optimal solution holds if the contribution to the profit of a Type B souvenir lies between $ 48 X and $ 96 X. (Enter your answers from smallest to largest.) (b) Find the contribution to the profit of a Type A souvenir (with the contribution to the profit of a Type B souvenir held at $1.20), given that the optimal profit of the company will be $196.80. $2 (c) What will be the optimal profit of the company if the contribution to the profit of a Type B souvenir is $1.50 (with the contribution to the profit of a Type A souvenir held at $1.00)? $168arrow_forwardKane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $1.75, and the profit for each model B grate is $1.25. Available for grate production each day are 1000 pounds of cast iron and 20 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day. Maximize P = 1.75x + 1.25y subject to 3x + 4y ≤ 1000 Resource 1 6x + 3y ≤ 1200 Resource 2 x ≤ 180 Resource 3 y ≥ 0 x ≥ 0 (a) Find the shadow price for Resource 2. (Round your answer to the nearest cent.)$ (b) Identify the binding and nonbinding constraints. constraint 1 constraint 2 constraint 3arrow_forwardKane Manufacturing has a division that produces two models of grates, model A and model B. To produce each model A grate requires 3 pounds of cast iron and 6 minutes of labor. To produce each model B grate requires 4 pounds of cast iron and 3 minutes of labor. The profit for each model A grate is $2.00, and the profit for each model B grate is $1.50. Available for grate production each day are 1000 pounds of cast iron and 20 labor-hours. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 180 grates per day. Maximize P = 2x + 1.5y subject to 3x + 4y ≤ 1000 Resource 1 6x + 3y ≤ 1200 Resource 2 x ≤ 180 Resource 3 y ≥ 0 x ≥ 0 (a) Find the shadow price for Resource 2. (Round your answer to the nearest cent.)$ (b) Identify the binding and nonbinding constraints. constraint 1 constraint 2 constraint 3arrow_forward
- A manufacturer produces two models of toy airplanes. It takes the manufacturer 32 minutes to assemble model A and 8 minutes to package it. It takes the manufacturer 20 minutes to assemble model B and 10 minutes to package it. In a given week, the total available time for assembling is 3200 minutes, and the total available time for packaging is 960 minutes. Model A earns a profit of $10 for each unit sold and model B earns a profit of $8 for each unit sold. Assuming the manufacturer is able to sell as many models as it makes, how many units of each model should be produced to maximize the profit for the given week? Note that the ALEKS graphing calculator can be used to make computations easier. k trol Model A: unit(s) Model B: unit(s) Continue 1 Q A 2 option X NO 2 Z W S 5 # 3 ME P X E H command $ 4 D 9 R C % 5 F T A V 6 FO G Y 8 7 B Submit A © 2023 McGraw HRLLC Al Rights Reserved forms of Use | Plicy Center the # WY 8 U Deft FN J N 3 9 K M O < P 1 garrow_forwardA carpenter builds bookshelves and tables for a living. Each bookshelf takes one box of screws, two 2 ✕ 4's, and three sheets of plywood to make. Each table takes two boxes of screws, four 2 ✕ 4's, and four sheets of plywood. The carpenter has 80 boxes of screws, 145 2 ✕ 4's, and 170 sheets of plywood on hand. In order to maximize their profit using these materials on hand, the carpenter has determined that they must build 12 shelves and 29 tables. How many of each of the materials (boxes of screws, 2 ✕ 4's, and sheets of plywood) are leftover, when the carpenter builds 12 shelves and 29 tables? The carpenter has boxes of screws, 2 ✕ 4's, and sheets of plywood leftover.arrow_forwardSuppose that a small company produces two different models of kayaks. A larger model and smaller model. The larger model requires 2 hours of manufacturing, 2 hours for assembly and 3 hours for packaging. The smaller model requires 2 hours for manufacturing, 1 hour for assembly and 2 hours for packaging. Each week the company has 120 hours available for manufacturing, 80 hours available for assembly and 132 hours available for packaging. If the company makes a profit of $75 for each of the larger model manufactured and profit of $60 for each smaller model manufactured, how many of each model should the company produce in order to maximize profit ?arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






