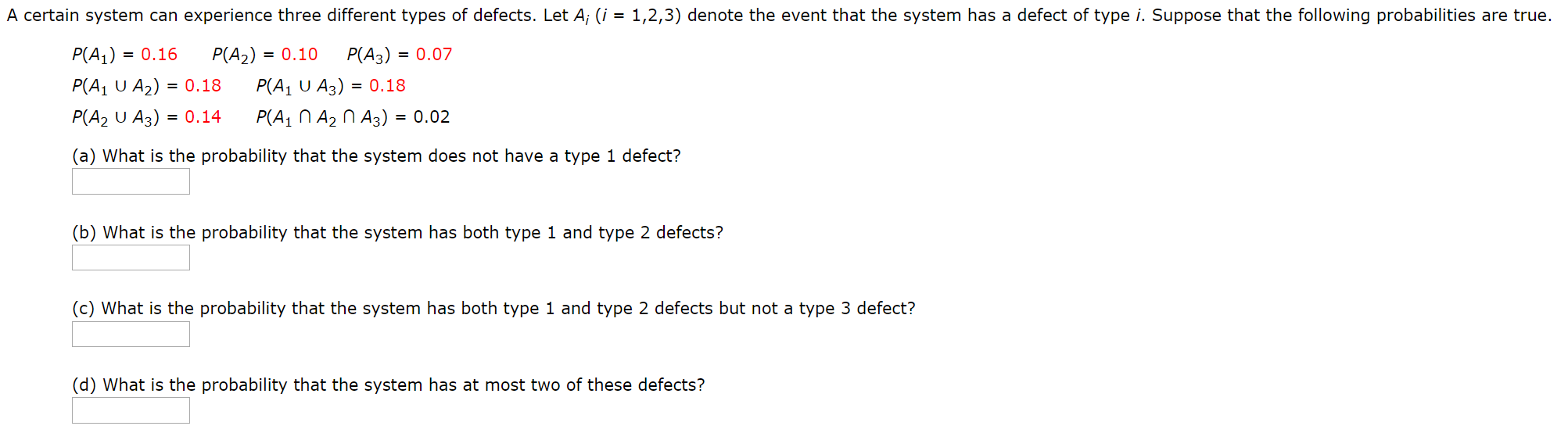
A certain system can experience three different types of defects. Let A; (i = 1,2,3) denote the event that the system has a defect of type i. Suppose that the following probabilities are true.P(A3) = 0.07P(A1) = 0.16P(A2) = 0.10P(A1 U A3) = 0.18P(A1 U A2) = 0.18P(A2 U A3) = 0.14P(A1 N A2 N A3) = 0.02(a) What is the probability that the system does not have a type 1 defect?(b) What is the probability that the system has both type 1 and type 2 defects?(c) What is the probability that the system has both type 1 and type 2 defects but not a type 3 defect?(d) What is the probability that the system has at most two of these defects?

Hello there! there are more than three subparts in the question. According to our policies we cannot…

Answered: A certain system can experience three…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Similar questions

There are three kinds of vegetation in an ecosystem: grass (G), shrubs (S), and trees (T) (Bodine, Lenhart, and Gross 2014). Every year, 25% of grassland plots are converted to shrubs, 20% of shrub plots are converted to trees, 8% of trees are converted to shrubs, and 1% of trees are converted to grass; the other transition probabilities are 0. Calculate the probability of a plot of land have the following succession of vegetation from year to year: GSGG, taking the first state as given. (type three digits after the decimal).
The PMF of the number of components K of a system that fails is defined by = {( PK (k)= ()(0.2)*(0.8) 4-k k= 0, 1,...,4 otherwise (a) What is the CDF of K? (b) What is the probability that fewer than two components of the system fail?
The prior probabilities for events A1, A2, and A3 are P(A1) = 0.20, P(A2) = 0.30, and P(A3) = 0.50. The conditional probabilities of event B given A1, A2, and A3 are P(B | A1) = 0.50, P(B | A2) = 0.30, and P(B | A3) = 0.40. (Assume that A1, A2, and A3 are mutually exclusive events whose union is the entire sample space.) (a) Compute P(B ∩ A1), P(B ∩ A2), and P(B ∩ A3). P(B ∩ A1) = P(B ∩ A2) = P(B ∩ A3) = (b) Apply Bayes' theorem, P(Ai | B) = P(Ai)P(B | Ai) P(A1)P(B | A1) + P(A2)P(B | A2) + + P(An)P(B | An) , to compute the posterior probability P(A2 | B). (Round your answer to two decimal places.) (c) Use the tabular approach to applying Bayes' theorem to compute P(A1 | B), P(A2 | B), and P(A3 | B). (Round your answers to two decimal places.) Events P(Ai) P(B | Ai) P(Ai ∩ B) P(Ai | B) A1 0.20 0.50 A2 0.30 0.30 A3 0.50 0.40 1.00 1.00
A sample is selected from one of two populations, S, and S₂, with P(S₁) = 0.6 and P(S₂) = 0.4. The probabilities that an event A occurs, given that event S, or S₂ has occurred are P(A|S₂) = = 0.4 and P(AIS₂) = 0.3 and the probability of event A is P(A) = 0.36. Use Bayes' Rule to find P(S, IA). (Round your answer to four decimal places.)
i need detailed solution
The prior probabilities for events A₁, A2, and A3 are P(A₁) = 0.20, P(A₂) = 0.30, and P(A3) = 0.50. The conditional probabilities of event B given A₁, A₂, and A3 are P(B | A₁) = 0.50, P(B | A₂) = 0.30, and P(B | A3) = 0.40. (Assume that A₁, A₂, and A3 are mutually exclusive events whose union is the entire sample space.) (a) Compute P(B ŉ A₁), P(B n A₂), and P(B n A3). P(B n A₁) P(B n A₂) = P(B n A3) = P(A₁)P(B | A₁) (b) Apply Bayes' theorem, P(A¡ | B) = 7 to compute the posterior probability P(A₂ | B). (Round your answer to two decimal P(A₁)P(B | A₁) + P(A₂)P(B | A₂) + + P(An)P(B | An)' places.) (c) Use the tabular approach to applying Bayes' theorem to compute P(A₁ | B), P(A₂ | B), and P(A3 | B). (Round your answers to two decimal places.) Events P(A₁) | P(B | A;) P(A¡n B) P(A¡ | B) A₁ 0.20 0.50 A₂ 0.30 0.30 A3 0.50 0.40 1.00 1.00 0.00
A certain system can experience three different types of defects. Let Ai (i = 1,2,3) denote the event that the system has a defect of type i. Suppose that the following probabilities are true. P(A1) = 0.10 P(A2) = 0.07 P(A3) = 0.06P(A1 ∪ A2) = 0.11 P(A1 ∪ A3) = 0.13P(A2 ∪ A3) = 0.11 P(A1 ∩ A2 ∩ A3) = 0.01 (c) Given that the system has at least one type of defect, what is the probability that it has exactly one type of defect? (Round your answer to four decimal places.) (d) Given that the system has both of the first two types of defects, what is the probability that it does not have the third type of defect? (Round your answer to four decimal places.)
S P(A/B): A Let event A = Student belongs to at least one club on campus and event B = Student participates in team sports on campus P(B|A) = ANB At AnyTown Polytechnic College, 42% of students belong to a campus club, 38% of students participate in team sports, and 5% belong to at least one campus club and participate in team sports. Compute the probabilities requested below. Round all probabilities to four decimal places, as needed. P(ANB) = P(AnB): B
A nuclear reactor becomes unstable if both safety mechanisms A and B fail. The probabilities of failure are P(A) =1/300 and P(B) = 1/200. Also, if A has failed, B is then more likely to fail: P(B/A)=1/100. a) What is the probability of the reactor going unstable? b) If B has failed, what is the probability of the reactor going unstable?
A machine has four components, A, B, C, and D, set up in such a manner that all four parts must work for the machine to work properly. Assume the probability of one part working does not depend on the functionality of any of the other parts. Also assume that the probabilities of the individual parts working are P(A) = P(B) = 0.95, P(C) = 0.91, and P(D) = 0.96. Find the probability that at least one of the four parts will work. Round to six decimal places.
Consider purchasing a system of audio components consisting of a receiver, a pair of speakers, and a CD player. Let A₁ be the event that the receiver functions properly throughout the warranty period, A₂ be the event that the speakers function properly throughout the warranty period, and A3 be the event that the CD player functions properly throughout the warranty period. Suppose that these events are (mutually) independent with P(A₁) = 0.92, P(A₂) = 0.96, and P(A3) = 0.90. (Round your answers to four decimal places.) (a) What is the probability that all three components function properly throughout the warranty period? (b) What is the probability that at least one component needs service during the warranty period? (c) What is the probability that all three components need service during the warranty period? (d) What is the probability that only the receiver needs service during the warranty period? (e) What is the probability that exactly one of the three components needs service…
1. The picture's river has floodgates at points A, B, C and D. The probabilities of each of the floodgates being open (a requirement for water to pass through) are the following: A: 94%, B : 96%, C: 91%, D: 97% The probabilities of the floodgates being open are independent. What is the probability that the water from the leftmost point in the picture will reach the sea on the right? C D B THE SEAL

Recommended textbooks for you

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

MATLAB: An Introduction with Applications

Statistics

ISBN:

9781119256830

Author:

Amos Gilat

Publisher:

John Wiley & Sons Inc

Probability and Statistics for Engineering and th…

Statistics

ISBN:

9781305251809

Author:

Jay L. Devore

Publisher:

Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…

Statistics

ISBN:

9781305504912

Author:

Frederick J Gravetter, Larry B. Wallnau

Publisher:

Cengage Learning

Elementary Statistics: Picturing the World (7th E…

Statistics

ISBN:

9780134683416

Author:

Ron Larson, Betsy Farber

Publisher:

PEARSON

The Basic Practice of Statistics

Statistics

ISBN:

9781319042578

Author:

David S. Moore, William I. Notz, Michael A. Fligner

Publisher:

W. H. Freeman

Introduction to the Practice of Statistics

Statistics

ISBN:

9781319013387

Author:

David S. Moore, George P. McCabe, Bruce A. Craig

Publisher:

W. H. Freeman

SEE MORE TEXTBOOKS