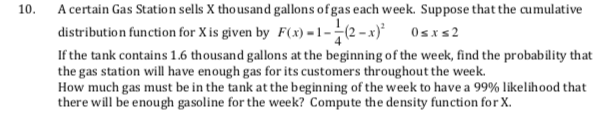
A certain Gas Station sells X thousand gallons of gas each week. Suppose that the cumulativedistribution function for X is given by F(x) =1–-(2 – x)*10.Osxs2If the tank contains 1.6 thousand gallons at the beginning of the week, find the probability thatthe gas station will have enough gas for its customers throughout the week.How much gas must be in the tank at the beginning of the week to have a 99% likelihood thatthere will be enough gasoline for the week? Compute the density function for X. o = 100 if theScores on a school's entrance exam are normally distributed with u= 500school wishes to admit only the students in the top 40% what should be the cutoff grade?15.

Answered: A certain Gas Station sells X thousand…

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Similar questions

a, b, d,
Today, the waves are crashing onto the beach every 4.4 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 4.4 seconds. Round to 4 decimal places where possible. The probability that the wave will crash onto the beach between 1.2 and 2.1 seconds after the person arrives is P(1.2 < x < 2.1) = The probability that it will take longer than 3.28 seconds for the wave to crash onto the beach after the person arrives is P(x > 3.28) = Suppose that the person has already been standing at the shoreline for 0.7 seconds without a wave crashing in. Find the probability that it will take between 3 and 3.7 seconds for the wave to crash onto the shoreline. 62% of the time a person will wait at least how long before the wave crashes in? seconds. Find the minimum for the upper quartile. seconds. Hint:
b. The lifetime X of a particular species is assumed to be exponentially distributed with mean 75 time units. Find the probability that a member of this particular species picked at random survives: i. more than 90 time units; less than 70 time units; between 70 and 85 time units. ii. iii. iv. Calculate Var(X).
Suppose model (XY, XZ, YZ) holds in a 2 x 2 x 2 table, and the common XY conditional log odds ratio at the two levels of Z is positive If the XY and YZ conditional log odds ratios are both positive or both negative, show that the XY marginal odds ratio is larger than the XY conditional odds ratio.
Today, the waves are crashing onto the beach every 5.1 seconds. The times from when a person arrives at the shoreline until a crashing wave is observed follows a Uniform distribution from 0 to 5.1 seconds. Round to 4 decimal places where possible. The probability that a person will be born between weeks 18 and 52 is P(18<x<52)P(18<x<52) = The probability that a person will be born after week 40 is P(x > 40) = P(x > 10 | x < 47) =
The level of nitrogen oxides (NOX) and nonmethane organic gas (NMOG) in the exhaust over the useful life (150,000150,000 miles of driving) of cars of a particular model varies Normally with mean 8080 mg/mi and standard deviation 66 mg/mi. A company has 1616 cars of this model in its fleet. Using Table A, find the level ?L such that the probability that the average NOX + NMOG level ?¯x¯ for the fleet greater than ?L is only 0.030.03 ? (Enter your answer rounded to three decimal places. If you are using CrunchIt, adjust the default precision under Preferences as necessary. See the instructional video on how to adjust precision settings.)
The time between failures of our video streaming service follows an exponential distribution with a mean of 40 days. Our servers have been running for 17 days, What is the probability that they will run for at least 97 days? (clarification: run for at least another 80 days given that they have been running 17 days). Report your answer to 3 decimal places.
Prob and stat
Suppose the lifespan (in months) of a smartphone battery can be modeled as a continuous random variable with CDF F(x) = 1 − e-x/3 x ≥ 0 What is the probability that the battery lasts between 12 to 15 months?
The life X (in hours) of a battery in constant use is a random variable with exponential density. What is the probability that the battery will last more than 12 hours (h) if the average life is 8 h?
I need to figure out the probability that component proportions produce the results X1 < 0.2 and X2 > 0.5 but I need help.

Recommended textbooks for you

A First Course in Probability (10th Edition)

Probability

ISBN:

9780134753119

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability

Probability

ISBN:

9780321794772

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability (10th Edition)

Probability

ISBN:

9780134753119

Author:

Sheldon Ross

Publisher:

PEARSON

A First Course in Probability

Probability

ISBN:

9780321794772

Author:

Sheldon Ross

Publisher:

PEARSON

SEE MORE TEXTBOOKS