College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
A beam of white light is incident on the surface of a diamond at an angle θa�a.(Figure 1) Since the index of refraction depends on the light's wavelength, the different colors that comprise white light will spread out as they pass through the diamond. The indices of refraction in diamond are nred=2.410�red=2.410 for red light and nblue=2.450�blue=2.450 for blue light. The surrounding air has nair=1.000�air=1.000. Note that the angles in the figure are not to scale.
![## Part C
**Objective:**
Derive a formula for \(\delta\), the angle between the red and blue refracted rays in the diamond.
**Instructions:**
Express the angle in terms of \(n_{\text{red}}, n_{\text{blue}},\) and \(\theta_a\). Use \(n_{\text{air}} = 1\). Note that any trig function entered in your answer must be followed by an argument in parentheses.
**Formula:**
\[
\delta = \sin^{-1}\left(\frac{\sin\theta_{\text{air}}}{n_{\text{red}}}\right) - \sin^{-1}\left(\frac{\sin\theta_{\text{air}}}{n_{\text{blue}}}\right)
\]
**Interface Elements:**
- **Button Labels:**
- **Submit**: Finalize your answer.
- **Previous Answers**: Review past responses.
**Additional Resources:**
- **Hints:** Access via “View Available Hint(s)" for guidance.
- **Keyboard Shortcuts:** Optimize input efficiency.
- **Undo/Redo/Reset Options:** Easily correct or restart the input process.](https://content.bartleby.com/qna-images/question/4d7adbf1-3ca3-4012-a27a-9468e79345de/0ab7301c-2193-460b-8423-1d9b80cff512/tdkgypg_processed.png)
Transcribed Image Text:## Part C
**Objective:**
Derive a formula for \(\delta\), the angle between the red and blue refracted rays in the diamond.
**Instructions:**
Express the angle in terms of \(n_{\text{red}}, n_{\text{blue}},\) and \(\theta_a\). Use \(n_{\text{air}} = 1\). Note that any trig function entered in your answer must be followed by an argument in parentheses.
**Formula:**
\[
\delta = \sin^{-1}\left(\frac{\sin\theta_{\text{air}}}{n_{\text{red}}}\right) - \sin^{-1}\left(\frac{\sin\theta_{\text{air}}}{n_{\text{blue}}}\right)
\]
**Interface Elements:**
- **Button Labels:**
- **Submit**: Finalize your answer.
- **Previous Answers**: Review past responses.
**Additional Resources:**
- **Hints:** Access via “View Available Hint(s)" for guidance.
- **Keyboard Shortcuts:** Optimize input efficiency.
- **Undo/Redo/Reset Options:** Easily correct or restart the input process.
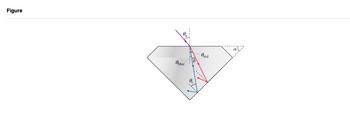
Transcribed Image Text:### Figure Explanation
This diagram illustrates the refraction and dispersion of light as it passes through a prism-shaped object, commonly used to demonstrate the separation of light into its various color components (spectrum).
#### Components Explained:
- **Incident Ray**: The initial light ray entering the prism is represented by a pink arrow labeled with the angle \( \theta_a \). This angle is measured between the incident ray and the normal to the prism surface.
- **Refracted Ray**: As the light enters the prism, it refracts, bending towards the normal. The internal angles, \( \theta_{\text{blue}} \) and \( \theta_{\text{red}} \), are the angles of refraction for blue and red light, respectively. These are depicted as a blue and red arrow inside the prism.
- **Dispersion**: The separation of light into colors is shown by two distinct paths inside the prism:
- **Blue Light Path**: Refracts at a sharper angle (\( \theta_{\text{blue}} \)) due to having a shorter wavelength.
- **Red Light Path**: Refracts at a lesser angle (\( \theta_{\text{red}} \)) as it has a longer wavelength.
- **Critical Angle (\( \theta_c \))**: This is the angle of incidence above which total internal reflection occurs rather than refraction. It is marked near the largest angle inside the prism.
- **Angle of Deviation (\( \delta \))**: The change in direction of the light ray as it passes through the prism. This is the angle between the original path of the incoming beam and the path of the outgoing refracted beam.
- **Prism Angle (\( \alpha \))**: The angle of the prism itself, shown as a dotted line forming the apex of the triangular prism shape.
This diagram serves to explain how light behaves as it transitions between different media, specifically how it separates into various colors (dispersion) due to differences in wavelength. This principle is the basis for various optical instruments and phenomena.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A beam of white light is incident on the surface of a diamond at an angle a.( Figure 1) Since the index of refraction depends on the light's wavelength, the different colors that comprise white light will spread out as they pass through the diamond. The indices of refraction in diamond are nred= 2.410 for red light and nblue = 2.450 for blue light. The surrounding air has nair = 1.000. Note that the angles in the figure are not to scale. Figure Oplue Ored α 1 of 1 Part A Calculate vred, the speed of red light in the diamond. To four significant figures, c = 2.998 × 108 m/s. Express your answer in meters per second to four significant digits. VE ΑΣΦ Ured= Submit Part B Ublue = Submit Part C Calculate blue, the speed of blue light in the diamond. To four significant figures, c = 2.998 × 108 m/s. Express your answer in meters per second to four significant digits. —| ΑΣΦ Request Answer 8 = Submit 2 Request Answer ? ? m/s ? Derive a formula for S, the angle between the red and blue…arrow_forwardWhite light is incident from air onto a triangular prism at a 55.0º angle with respect to the normal. The prism has an index of refraction of 1.45 for red light and 1.50 for violet light and the apex angle of the prism is 60º. Take nair=1.00 for all wavelengths.a) What is the angular separation (dispersion angle) of the two ends of the visible spectrum while in the prism? b) What is the angular separation (dispersion angle) of the two ends of the visible spectrum upon exiting the prism?arrow_forwardLight is incident from vacuum to crown glass; the light's vacuum wavelength is 500 nm, so the refractive index is 1.52 for crown glass. If the light is incident at an angle of 25.0o, what is the angle of light with respect to the normal once its has entered the crown glass? Answer in degrees.arrow_forward
- A ray of monochromatic light travels from oil into crown glass (nglass= 1.25) at an angle of 55.0⁰. If the angle in glass is 65.0", what is the index of refraction of the oil?arrow_forwardThe index of refraction of silicate flint glass for red light is 1.620 and for violet light is 1.660. A beam of white light in this glass strikes the glass-air interface at 20.10 angle of incidence and refracts out into the air. What is the angular separation between the red and violet components of the spectrum that emerges from the glass?arrow_forwardattachedarrow_forward
- A beam of light with wavelength X = 470 nanometers traveling in air (index of refraction n=1) enters a new medium with index of refraction n=1.35. What is the wavelength of light inside the new medium? (give your answer in nanometers)arrow_forwardImmiscible liquids (ones that do not mix) can be placed on top of each other in a glass. Each layer may have a different refractive index. If we shine a ray down from the air above into the glass on the left at an angle of 3.8 degrees from the vertical, what is the angle of the light when it reaches the bottom of the glass? (Units: degrees) n (air) 1.00 n (lamp oil) 1.51 n (rubbing alcohol) 1.39 n (vegetable oil) 1.45 n (water) 1.33 n (dish soap) 1.35arrow_forwardA fiber optic is made by cladding a thin fiber core of refractive index n₁ = 1.45 with a material of refractive index n₂ = 1.38. What is the maximum incident angle, 0, so that the light ray is totally internally reflected inside the fiber?arrow_forward
- A beam of white light enters the glass and forms a red and blue component. The refractive index of blue light for the glass is found to be 1.536 and for red light 1.507. The angle of incidence is measured to be 40.5. With this data calculate the angle between the red and blue components of the light.arrow_forwardA beam of white light is incident on the surface of a diamond at an angle θa. (Figure 1) Since the index of refraction depends on the light's wavelength, the different colors that comprise white light will spread out as they pass through the diamond. For example, the indices of refraction in diamond are nred=2.410for red light and nblue=2.450blue=2.450 for blue light. Thus, blue light and red light are refracted at different angles inside the diamond, as shown in the picture. The surrounding air has nair=1.000 Note that the angles in the figure are not to scale. Now consider θc, the angle at which the blue refracted ray hits the bottom surface of the diamond. If θc is larger than the critical angle θcrit, the light will not be refracted out into the air, but instead it will be totally internally reflected back into the diamond. Find θcrit.arrow_forwardA beam of light is incident at 30° on a piece of glass in air. The dispersion of colours spans 1 mm on the bottom surface of the glass as shown below. The thickness of the glass slab is L = 10 cm. The index of refraction for red light is n_red = 1.513. Detemine the index of refraction for violet light. 30° Red. 1 mm n_violet = 1.624 n_violet = 1.511 n_violet = 1.553 O n_violet = 1.651 n_violet = 1.433arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON