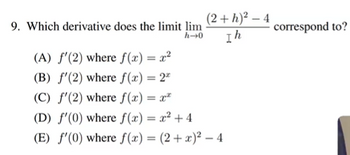
9. Which derivative does the limit lim h→0 (2+h)²2-4 Ih (A) f'(2) where f(x) = x² (B) f'(2) where f(x) = 2* (C) f'(2) where f(x) = x (D) f'(0) where f(x) = x² + 4 (E) f'(0) where f(x) = (2+ x)² - 4 correspond to?

1. For each function given below, calculate the derivative at a point f'(a) using the limit definition. (a) f(x) = 2x2 – 3r f'(0) =? (b) f(x) = /2x + I f'(4) =? 1 (c) f(x)= f'(3) =? x - 2 (d) f(x)= (x – 3)3 f'(4) =? 2. For each function f(x) given below, find the general derivative f' (x) as a new function by using the limit definition. (a) f(x) = V – 4 f'(x) =? (b) f(x)= -r³3 f'(x) =? (c) f(r) = f'(x) =? 3x + 1 1 (d) f(x) = f'(x) =? %3D 3. For each function f(x) given below, find the equation of the tangent line at the indicated point. (a) f(x)= x – r² at (2, –2) (b) f(x) = 1– 3r2 at (0, 1) 1 f(x) = 2r (c) at x = 1 (d) f(x) = x + VI at x = 1 4. Given f(x) = ax² + 2x and f'(1) = 5, solve for a.

Given f(x) = 4, find f'(x) using the limit definition of the derivative. f(x + h) = f(x +h)-f(x) = f(x+h)-f(x) h f'(x) = lim h→0 f(x +h)-f(x) h = O 0 O 0 of 0