
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
Please answer the question providing all steps and clear writing so I can understand. Thanks.
You can see as a Reference book "James Stewart Calculus 8th Edition" to see similar solutions
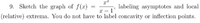
Transcribed Image Text:### Problem 9
#### Task:
Sketch the graph of the function \( f(x) = \dfrac{x^2}{x-1} \). Label the asymptotes and local (relative) extrema. You do not have to label concavity or inflection points.
#### Detailed Steps:
1. **Find the Asymptotes:**
- **Vertical Asymptote:** Set the denominator equal to zero and solve for \( x \). The vertical asymptote is at \( x = 1 \).
- **Horizontal Asymptote:** Analyze the degrees of the numerator and the denominator. Since the degree of the numerator (2) is greater than the degree of the denominator (1), there is no horizontal asymptote. Instead, check for an oblique asymptote by performing polynomial long division.
2. **Determine the Local Extrema:**
- Find the first derivative \( f'(x) \) to determine the critical points.
- Set \( f'(x) = 0 \) and solve for \( x \).
- Use the second derivative test or the first derivative test to confirm whether these points are local maxima or minima.
3. **Plot Key Points and Asymptotes:**
- Draw the vertical asymptote at \( x = 1 \).
- Plot any calculated critical points.
- Draw the graph based on the identified behavior, ensuring it approaches the asymptotes appropriately.
For detailed calculations and the sketch, students are encouraged to work through the derivations and plotting individually or refer to supplemental graphing tools or software.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

