
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question

Transcribed Image Text:### Geometry Problem: Tangent Lines and Circle Intersections
#### Problem Statement
9. Lines \(AE\) and \(BD\) are tangent to circles \(O\) and \(P\) at \(A\), \(E\), \(B\), and \(D\), as shown in the diagram below. If \(AC : CE = 5 : 3\) and \(BD = 56\), determine and state the length of \(CD\).
#### Diagram Description:
The diagram depicts two circles that are externally tangent to each other. There are four lines extending tangentially from points where the circles touch these lines. The setup can be described as follows:
- Circle \(O\) is tangent to line \(AE\) at point \(A\) and to line \(BD\) at point \(B\).
- Circle \(P\) is tangent to line \(AE\) at point \(E\) and to line \(BD\) at point \(D\).
- The circles touch each other at their point of tangency, labeled \(C\).
- The ratio of segments \(AC\) to \(CE\) is given as \(5 : 3\).
- The total length of line \(BD\) is provided as \(56\).
#### Solution Approach
To solve for the length of \(CD\), apply geometric properties of tangents and the given ratio. Utilize the information given and relationships between the points, tangents, and circles to determine the segment length accurately.
### Educational Resources
Explore more on similar geometric problems and detailed explanations on tangents and circle interactions by visiting our additional resources and problem sets.
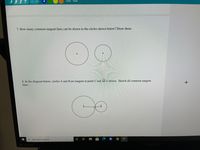
Transcribed Image Text:### Geometry: Tangents to Circles
#### Problem 7
**Question:** How many common tangent lines can be drawn to the circles shown below? Draw them.
**Description:**
This problem involves two separate circles placed in a plane. The task is to determine the number of common tangent lines that can be drawn to these circles and illustrate these lines.
*Diagrams:*
- The diagram consists of two separate circles.
- Circle 1 is on the left side and Circle 2 is on the right side. Both circles are not intersecting each other nor are they tangent to each other.
- Each circle has a small dot in the center representing the center of the circle.
*Explanation:*
- External tangents: Lines that touch both circles at different points on their respective circumferences.
- Internal tangents: Lines that touch both circles but pass between them.
#### Problem 8
**Question:** In the diagram below, circles A and B are tangent at point C and AB is drawn. Sketch all common tangent lines.
**Description:**
This problem involves two circles, A and B, which are tangent to each other at a single point C. The line segment AB is the line connecting the centers of the two circles. The task is to sketch all the common tangent lines to these circles.
*Diagrams:*
- The diagram shows two circles tangent to each other at a single point labeled C.
- Circle A is on the left side and Circle B is on the right side.
- The center of Circle A is marked with an A, and the center of Circle B is marked with a B.
- A line AB connects the centers of the two circles, indicating their line of centers.
*Explanation:*
- External tangents: Lines that touch both circles at different points on their circumferences without intersecting the area between the circles.
- Internal tangents: Lines that touch both circles but pass through the area where the circles meet.
Illustrations provided assist in understanding the nature of tangent lines between two circles depending on their configuration in the plane.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Determine if line AB is tangent to the circle. 1) 2) B 6.6 8 16 12 11 13 3) 4) 12 16 11.4 20 19 A 15.2 Barrow_forward5. In the diagram below of circle O, chords 7R and AB intersect at E. CD If CE = 10, ED = 6 and AE = 4, what is the length of ЕВ A 2.4 B. 6.7 C. 12 D. 15arrow_forward2. Find the missing angles labelled in each of these circles. a. 31° b. Ý SOE BỘ 80+2 90-y 2x+4 C. 12cm Scmyarrow_forward
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning