
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Calculus 2 HW
Please calculate the improper
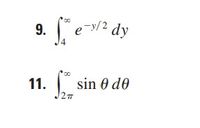
Transcribed Image Text:Certainly! Here are the transcriptions of the integrals shown in the image:
9. \(\int_{4}^{\infty} e^{-y/2} \, dy\)
11. \(\int_{2\pi}^{\infty} \sin \theta \, d\theta\)
These integrals are both improper, extending to infinity as one of their limits. The first represents the integration of an exponential decay function, while the second involves the sine trigonometric function.
- **Integral 9** requires evaluating the behavior of the exponential function, which generally decreases towards zero as \(y\) increases.
- **Integral 11** involves the periodic sine function, which oscillates indefinitely, requiring consideration of its convergence or divergence over the specified interval.
![### Transcription
#### Integrals
5. Evaluate the integral:
\[
\int_{3}^{\infty} \frac{1}{(x - 2)^{3/2}} \, dx
\]
6. Evaluate the integral:
\[
\int_{0}^{\infty} \frac{1}{\sqrt[4]{1 + x}} \, dx
\]
### Description
The image shows two mathematical integrals, which are common in calculus, where the goal is to determine the area under specific curves. Each integral has its respective bounds and integral function provided.
- **Integral 5**:
- The function is \(\frac{1}{(x - 2)^{3/2}}\), which potentially involves an improper integral due to its bounds going from 3 to \(\infty\). The term \((x - 2)^{3/2}\) implies a power function where \(x\) is offset by 2.
- **Integral 6**:
- The function is \(\frac{1}{\sqrt[4]{1 + x}}\). The interval of integration starts from 0 and extends to \(\infty\). The expression \(\sqrt[4]{1 + x}\) refers to the fourth root of the term \(1 + x\), indicating a radical function that grows at a rate determined by that root.](https://content.bartleby.com/qna-images/question/0e691e7d-3aa6-4d87-8ff6-0afc8b27fff3/efd08bee-994e-4fbd-ad39-2279dfef2e0d/1eos70di_thumbnail.jpeg)
Transcribed Image Text:### Transcription
#### Integrals
5. Evaluate the integral:
\[
\int_{3}^{\infty} \frac{1}{(x - 2)^{3/2}} \, dx
\]
6. Evaluate the integral:
\[
\int_{0}^{\infty} \frac{1}{\sqrt[4]{1 + x}} \, dx
\]
### Description
The image shows two mathematical integrals, which are common in calculus, where the goal is to determine the area under specific curves. Each integral has its respective bounds and integral function provided.
- **Integral 5**:
- The function is \(\frac{1}{(x - 2)^{3/2}}\), which potentially involves an improper integral due to its bounds going from 3 to \(\infty\). The term \((x - 2)^{3/2}\) implies a power function where \(x\) is offset by 2.
- **Integral 6**:
- The function is \(\frac{1}{\sqrt[4]{1 + x}}\). The interval of integration starts from 0 and extends to \(\infty\). The expression \(\sqrt[4]{1 + x}\) refers to the fourth root of the term \(1 + x\), indicating a radical function that grows at a rate determined by that root.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Hi I was wondering if you could walk me through a problem? The integral of x3*sqrt(x2+25)dx. Thanks!arrow_forwardEvaluate the integral using the Fundamental Theorem of Calculus Part 2. Reminder to leave the exact value (no decimal answers). 3 2sinx – ex dx -arrow_forwardHow do I solve this questionarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning