
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:(9)
(?)
(3) Let ei =
and e2 =
Let T be the linear transformation which sends e, to
( )
and sends e2 to
(a) Find the image of (
-3
and
X2
(b) What is the standard matrix of T?
(4) Let T : R² → R² be the linear transformation given by
r(:)-(,
(:)
xi + x2
4x1 + 5x2
T
X2
3
Find x such that Tx =
8
Expert Solution
arrow_forward
Step 1
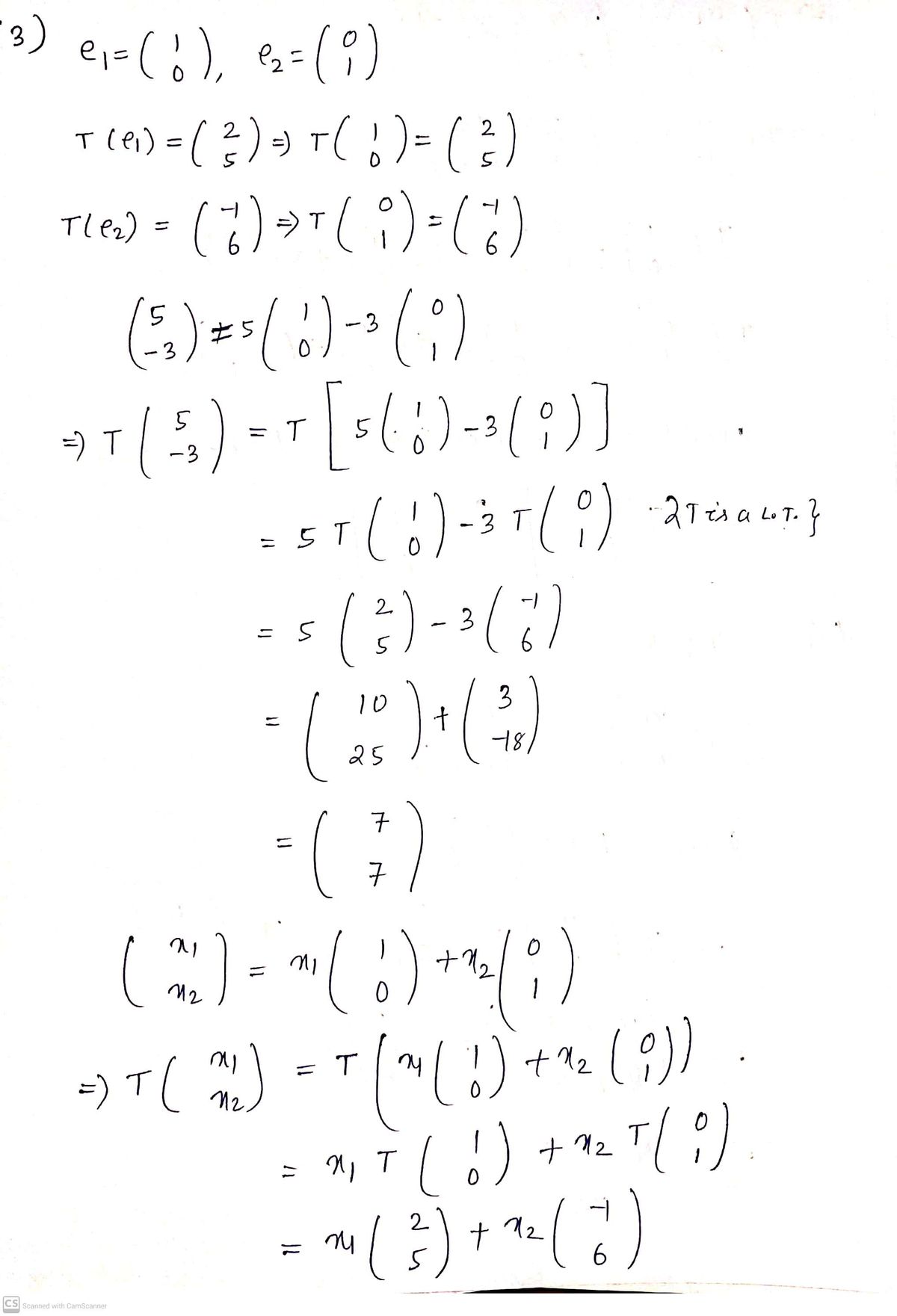
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- -2 Use a rectangular coordinate system to plot u = ,v = 1, and their images under the 4 -1 given transformation T(x) = | Describe geometrically what T does to each vector in R2.arrow_forward2. Let A = be an orthogonal 2 × 2 matrix. cos(0) sin(0 (a) Explain why the vector can be written as for some value of 0. a Use your answer to part (a) to find all 2×2 orthogonal matrices A = |C (b) (Hint: What can the second column of A look like?) (c) det(A) = 1? What kind of linear transformation do they correspond to? ! Given your answer to part (b), what are the 2 × 2 orthogonal matrices witharrow_forwardCross product is a linear transformation from R³ →R³ You can define it as X1 X2 X3 X Yı Y2 Y3 e₁ X1 Y1 x2 Y2 Y3 = = det( e2 → ez X3 Note that this is the determinant of a matrix that has vectors as some of the entries. You can look at section 3.6 in the textbook for alternate definitions. Define the linear transformation Tas T(x) = x x 2 3 a. Compute T(ei), T(₂), Te) b. Use your answer from a. to write the standard matrix of the linear transformation T c. Use your answer from b. to compute T( 4 H 3arrow_forward
- Find the matrix of the linear transformation T from R2 - R² where T([1, 0]) = [1, –2] and T([2, 1]) = [2, 3] %3D (Note: matrix A = [T([1, 0]), T([0, 1])] 1 -2 (a) 1 (b) 1 (c) -2 (d) -2 3 7 3 Ob a Carrow_forward3 1 Let TA: R2 R³ be the matrix transformation corresponding to A = 1 -2 5 ТA(u) 3 18 -1 = TA(V) X -1 4 Find TA(u) and TA(V), where u = 1 3 [2] and v = [-2]arrow_forward* (E)-E x1 +x2 Let the transformation T be given by T X2 %3D 2.x1 (a) Show that T is a linear transformation by finding a matrix that implements the mapping. (b) Show that the mapping is not onto by finding a vector in the codomain of T that is not in the range of T. Verify/show that your vector is not in the range of T.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

