Evaluate the surface integral R using the divergence theorem 8. Let F = xyzî + (y? + 1)ĵ + 2³k and S be the surface of the cube 0 < x, y, z < 1.(a) Evaluate the surface integral f Ss(V × F) · dS using the divergence theorem (hint:is there a helpful vector identity?).(b) Evaluate the surface integral S Ss(V x F) · dS using Stokes' theorem (hint: is therea boundary?)

Given that F→=xyzi→+y2+1j→+z3k→ S be the surface of the cube 0≤x,y,z≤1 Now,…

Answered: 8. Let F = xyzi + (y² + 1)ĵ + z³k and S…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Question

Evaluate the surface integral R using the divergence theorem

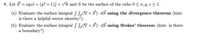
8. Let F = xyzî + (y? + 1)ĵ + 2³k and S be the surface of the cube 0 < x, y, z < 1.
(a) Evaluate the surface integral f Ss(V × F) · dS using the divergence theorem (hint:
is there a helpful vector identity?).
(b) Evaluate the surface integral S Ss(V x F) · dS using Stokes' theorem (hint: is there
a boundary?)

Expert Solution

Step 1

Given that

$\vec{F} = x y z \vec{i} + (y^{2} + 1) \vec{j} + z^{3} \vec{k}$

S be the surface of the cube $0 \leq x, y, z \leq 1$

Now,

$\nabla \times \vec{F} = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ x y z & y^{2} + 1 & z^{3} \end{matrix}| = \vec{i} (\frac{\partial}{\partial y} (z^{3}) - \frac{\partial}{\partial z} (y^{2} + 1)) - \vec{j} (\frac{\partial}{\partial x} (z^{3}) - \frac{\partial}{\partial z} (x y z)) + \vec{k} (\frac{\partial}{\partial x} (y^{2} + 1) - \frac{\partial}{\partial y} (x y z)) = 0 \vec{i} - j (0 - x y) + \vec{k} (0 - x z) \nabla \times \vec{F} = x y \vec{j} - x z \vec{k}$

a)Using divergence theorem,

$\iint_{S} \vec{F .} d \vec{S} = \int \int \int (\nabla \cdot \vec{F}) d \vec{S}$

Here,

$\iint_{S} (\nabla \times \vec{F}) d \vec{S} = \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} \nabla \cdot (\nabla \times \vec{F}) d \vec{S} = \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} (\frac{\partial}{\partial x} \vec{i} + \frac{\partial}{\partial y} \vec{j} + \frac{\partial}{\partial z} \vec{k}) . (x y \vec{j} - x z \vec{k}) d x d y d z = \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} (\frac{\partial}{\partial y} (x y) - \frac{\partial}{\partial z} (x z)) d x d y d z = \int_{0}^{1} \int_{0}^{1} \int_{0}^{1} (x - x) d x d y d z \iint_{S} (\nabla \times \vec{F}) d \vec{S} = 0$

Thus, the integral value becomes 0.

Step by step

Solved in 2 steps

Knowledge Booster

$Double Integration$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated