
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
Using basis and dimensions in
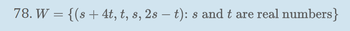
Transcribed Image Text:78. \( W = \{(s + 4t, t, s, 2s - t) : s \text{ and } t \text{ are real numbers}\} \)
This mathematical expression defines a set \( W \) consisting of ordered quadruples. Each quadruple is formed using the real numbers \( s \) and \( t \). The components of each quadruple are calculated as follows:
1. The first component is \( s + 4t \).
2. The second component is \( t \).
3. The third component is \( s \).
4. The fourth component is \( 2s - t \).
By varying the values of \( s \) and \( t \), you can generate all possible quadruples within the set \( W \). This set is defined in a 4-dimensional space, originating from the linear combination of the parameters \( s \) and \( t \).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- vector projectionarrow_forwardPlease give a clear and complete solution. Linear algebra and differential equationsarrow_forwardLinear Algebra Are the following sets V vector spaces? Prove or give a counter example.(a) V = R^2 and F = R where vector addition and scalar multiplication is defined as: (x_1, y_1) + (x_2, y_2) = (x_1 + y_2, y_1 + x_2), c(x_1, y_1) = (cx_1, cy_1).arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

