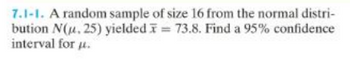
7.1-1. A random sample of size 16 from the normal distri- bution N(u. 25) yielded = 73.8. Find a 95% confidence interval for u.
Q: . Let X1, X2, . . . , X81 be a random sample from an unknown distribution. After observing this…
A:
Q: 9. We want to test Ho: μ = 1.5 Ha: 1.5 at a = 0.05. A 95% confidence interval for u calculated from…
A: 95% confidence interval is. (1.4 , 3.6)
Q: A random sample of size n, = 29, taken from a normal population with a standard deviation o, = 6,…
A: The confidence level is 0.96.
Q: Let two independent random samples, each of size 10, from two normaldistributions N(μ1, σ2) and…
A: A 1001-α% confidence interval on the difference is…
Q: 4.2.7: Let a random sample of size 17 from the normal distribution N(u, o²) yield = 4.7 and S2 =…
A:
Q: A random sample of 52 measurements was selected from a population with σ=3.6. The sample mean was…
A:
Q: A random sample of size 15 is taken from a normally distributed population with a sample mean of 75…
A: As population standard deviation is not known , the critical value can be calculated from student t…
Q: 4). Suppose that a random sample of size n = 16 from a normal population with mean µ and standard…
A: We have given that Sample size n=16 ,xbar=10.8 ,sigma =0.48 Alpha=0.05 Note:- According to…
Q: 9.2.12-T Question Help ▼ Independent random samples selected from two normal populations produced…
A: Given n1=17, X1bar=5.9, S1=3.7 n2=14, X2bar=7.9, S2=4.4 We want to find the test statistic and 95…
Q: Two types of plastic are suitable for an electronics component manufacturer to use. The breaking…
A: Given Data : For Sample 1 x̄1 = 162.5 σ1 = 1 n1 = 10 For Sample 2 x̄2 = 155…
Q: (4) We are told that a 95% prediction interval for a response variable, y, is [23.2, 35.6] from a…
A:
Q: A large candy manufacturer produces, packages and sells packs of candy targeted to weigh 52 grams. A…
A: In case of single population parameter comparison with a specific value with known population…
Q: For å distribution. The sample mean =14.5, sample variance =25, to.05.15=1.753. Then the upper bound…
A: From the given information we find the upper bound .
Q: A random sample of size n1 = 25 taken from a normal population with standard deviation of 5 has a…
A:
Q: Use The t Distribution Table to find the t/α2 value for a 95% confidence interval for the mean…
A: We have given that Confidence level (c) = 95% = 0.95 Significance level (α) = 1 - 0.95 = 0.05 Sample…
Q: 9.3.5 x Your answer incorrect. Try again. For the hypothesis test Ho : H = 24 against H :p < 24 with…
A:
Q: 1. Dr. Edgar Anderson was a botanist who collected vast amounts of data for several species of wild…
A: Since you have asked multiple question, we will solve the first question for you. If you want any…
Q: Testing Hu=4, H, : 4with the significance level a=0.05. (0.025=1.96)
A: Suppose that X~N(4,0.12). We have 16 random samples, and the sample mean is 3.92. Significance Level…
Q: 7.1-2. A random sample of size 8 from N(μ, 72) yielded x=85. Find the following confidence intervals…
A: According to the Bartleby guidelines expert solve only one question and maximum three subpart of the…
Q: Measurements of the length in centimeters of n = 29 fish yielded an average length of x = 16.82 and…
A: The given data is as follows:Sample size, Sample mean, Sample variance, Margin of error, Confidence…
Q: A simple random sample of size n is drawn from a population that is normally distributed. The sample…
A: Hello! As you have posted more than 3 sub parts, we are answering the first 3 sub-parts. In case…
Q: A sample of size 49 is drawn from a population where the population standard deviation is o = 4.8…
A: given data n = 49σ = 4.8x¯ = 1095 % ci for μ.Z = 1.96
Q: A sample of n = 100 scores is selected from a population with μ = 80 with σ = 20. On average, how…
A: Given information- Population mean, µ = 80 Population standard deviation, σ = 20 Sample size, n =…
Q: 4.42 A random sample of 400 is taken out of the more than 100,000 army recruits in a particular…
A:
Q: b) Let Y be the mean of sample of size n from a normal distribution with mean μ and variance 100. i.…
A:
Q: Two types of plastic are suitable for an electronics component manufacturer to use. The breaking…
A:
Q: Suppose a simple random sample of size n=40 is obtained from a population with μ=63 and σ=14.…
A:
Q: If the true variance, o? = 25. a. Construct a 95% two-sided confidence interval for u. Use Zo.025 =…
A:
Q: 2. We have a random sample of size 17 from the normal distribution N(µ,o²) where µ and o? are…
A:
Q: a) How much difference is there between the mean for the treated sample and the mean for the…
A: a) The sample size is 25, with sample mean 22.2, sums of squares is 384, and the population mean is…
Q: Consider a population with unknown mean u and un- known variance o? which is approximately normal.…
A:
Q: A sample of size n = 98 produced the sample mean of 22.1. Assuming the population standard…
A:
Q: A large candy manufacturer produces, packages and sells packs of candy targeted to weigh 52 grams. A…
A: It is given that Sample size n = 10 Sample variance = 4.2 Confidence level = 95%
Q: A simple random sample of size n=14 is obtained from a population with μ=67 and σ=19. Assuming…
A: From the given information, Consider, Sample size (n) = 14 Population with μ=67 and σ=19. Thus,
Q: 43. Independent random samples are selected from two populations. Below are selected summary…
A:
Q: Consider a normally distributed population of scores with a mean μ = 100 and σx = 10. What score has…
A:
Q: Suppose X is a random variable with normal distribution and Var(X)=100. Suppose we have a sample of…
A: The confidence level is 0.90.
Q: American Theatre owners knew that a certain hit movie ran an average of 84 days or more in each…
A: Any assumption about the parameter or probability function is known as Hypothesis testing. For the…
Q: standard deviations: Sample 1 Sample 2 17 12 n2 X2 X1 5.4 7.9 || S1 = 3.4 S2 4.8 variances, the a.…
A:
Q: A sample of n = 64 scores is selected from a population with µ = 80 and with σ = 24. On average, how…
A: Givenn=64μ=80σ=24
Q: A sample of n = 16 scores is selected from a population with μ = 100 and σ = 32. If the sample mean…
A: From the provided information,
Q: h penalty. If a random sample of n = 1234 ns yielded y = 864 who favored the death find an…
A: Sample size n =1234 Favorable cases y Sample proportion p^=y/n =864/1234 =0.7002
Q: the sample mean T= 0.73. Construct an approximate 95% confidence interval for p. This may be useful:…
A: A random variable X is called to follow the binomial distribution if it takes only non-negative…
![7.1-1 [71.35. 76.25].](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F2b62c17d-5c05-48d6-ac2b-a3a7c31907f7%2Ff9a7a48b-d05f-4dcf-aaeb-041522e7c7eb%2Fz8fqvle_processed.png&w=3840&q=75)
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images
- 7.. need help pleaseUse the t-distribution and the given sample results to complete the test of the given hypotheses. Assume the results come from random samples, and if the sample sizes are small, assume the underlying distributions are relatively normal. Test Ho : HA = Ha VS H. : HA # Hg using the fact that Group A has 8 cases with a mean of 125 and a standard deviation of 18 while Group B has 15 cases with a mean of 118 and a standard deviation of 14. (a) Give the test statistic and thep-value. Round your answer for the test statistic to two decimal places and your answer for the p- value to three decimal places. test statistic = p-value = eTextbook and Media (b) What is the conclusion of the test? Test at a 10% level. O Reject Ho. O Do not reject Ho. eTextbook and MediaQ2: Let x1,X2, . , Xn and y1, y2, ..., Ym represent two independent random samples from the respective normal distributions N(H1,07) and N (H2, 03). It is given that of = 30, but ožis unknown. Then 1. A random variable that can be used to find a 95% confidence interval for - is (x- y) - (H1 - H2) А. ns3 + ms n+m. 3(n+m-2)"tm, nm O A (x – y) – (41 – H2) В. ns? + ms; n + m. (n + m – - 2) пт (x – y) – (41 - H2) С. ns3 + mS;_n+3 3(n+ m-2) ("+3m nm Ос
- A sample of n 4 scores is selected from a population with an unknown mean. The sample has a mean of M= 40 and a variance of s² = 16. Which of the following is the correct 90% confidence interval for u? %3D O H = 40 + 1.638(4) O H = 40 + 2.353(4) OH= 40 + 1.638(2) Ομ= 40+ 2.353(2)Suppose a marketing company randomly surveyed 404 households and found that in 214 of them, the woman made the majority of the purchasing decisions. Construct a 90% confidence interval for the population proportion of households where the women make the majority of the purchasing decisions.p'=α2=zα2=Margin of Error: E=We are 90% confident that the proportion of households in the population where women make the majority of purchasing decisions is between___ and ___.Let X1, X2, X3, ..., X, be a random sample from a distribution with known variance Var(X,) = o², and unknown mean EX, = 0. Find a (1 – a) confidence interval for 0. Assume that n is large.
- Independent samples of size n1 = 25 and n2 = 36 are taken from two normal populations with knownstandard deviations of σ1 = 5.5 and σ2 = 4.2. e sample means are x¯1 = 13.6 and x¯2 = 19.2. Find a95% confidence interval for µ1 − µ2.Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from normally distributed populations. Also assume that the population standard deviations are equal (Η1 = Η2), so that the standard error of the difference between means is obtained by pooling the sample variances. 1) A paint manufacturer wanted to compare the drying times of two different types of paint.Independent simple random samples of 11 cans of type A and 9 cans of type B were selected andapplied to similar surfaces. The drying times, in hours, were recorded. The summary statistics areas follows.Type A Type Bx1 = 71.5 hr x2= 68.5 hrs1 = 3.4 hr s2 = 3.6 hrn1 = 11 n2 = 9a). Construct a 99% confidence interval for µ1- µ2, the difference between the mean drying timefor paint type A and the mean drying time for paint type B b). Run a hypt. test to determine the results*Alt is not equal*Make sure to select pooled…
