7. Let 1, 2, 3, 4 be the means of FOUR normal distributions with a common, but unknown, variance, ². In order to test, at the a=.01 significance level, the hypothesis Ho 1 = 2 = 3 = 44, we take a random sample of size five from each of these distributions. Determine whether Ho should be accepted or rejected, if the following values are the observed sample values: Distribution 1 2 3 16 19 23 10 11 20 15 13 25 21 19 29 26 19 28 24 31 12 16 22 A) Show the entire ANOVA table. B) Identify the critical region C) What is your decision for the hypothesis test? Justify your decision.
7. Let 1, 2, 3, 4 be the means of FOUR normal distributions with a common, but unknown, variance, ². In order to test, at the a=.01 significance level, the hypothesis Ho 1 = 2 = 3 = 44, we take a random sample of size five from each of these distributions. Determine whether Ho should be accepted or rejected, if the following values are the observed sample values: Distribution 1 2 3 16 19 23 10 11 20 15 13 25 21 19 29 26 19 28 24 31 12 16 22 A) Show the entire ANOVA table. B) Identify the critical region C) What is your decision for the hypothesis test? Justify your decision.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
Please help me solve for A,B,C.
![## Educational Website Content
### Analysis of Variance (ANOVA) Problem
**Problem Statement:**
Let \( \mu_1, \mu_2, \mu_3, \mu_4 \) be the means of four normal distributions with a common, but unknown, variance, \( \sigma^2 \). To test, at the \(\alpha = 0.01\) significance level, the hypothesis:
\[ H_0 : \mu_1 = \mu_2 = \mu_3 = \mu_4 \]
We take a random sample of size five from each of these distributions. Determine whether \( H_0 \) should be accepted or rejected, using the following observed sample values:
**Observed Sample Values:**
- Distribution 1: 12, 16, 19, 23, 10
- Distribution 2: 16, 11, 20, 15, 13
- Distribution 3: 25, 21, 19, 29, 26
- Distribution 4: 22, 19, 28, 24, 31
### Tasks:
**A) Show the entire ANOVA table.**
Construct an ANOVA table that includes the sources of variation, sum of squares, degrees of freedom, mean squares, and the F-ratio.
**B) Identify the Critical Region**
Determine the critical region based on the F-distribution with the appropriate degrees of freedom and significance level (\(\alpha = 0.01\)).
**C) Decision for the Hypothesis Test**
Make a decision for the hypothesis test. Should the null hypothesis \( H_0 \) be accepted or rejected? Justify your decision based on the calculated F-ratio and the critical value.
### Additional Information:
- **Diagram** or **Graph Explanation**: No diagrams or graphs are present in the problem.
- Use statistical software or manual calculations to complete the ANOVA table and hypothesis test.
- Make sure to verify calculations for accuracy, as the problem stems from a typical scenario in statistics involving hypothesis testing using ANOVA.
This problem helps in understanding the application of ANOVA in testing the equality of means from multiple groups with a given statistical significance level.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F9ad7648d-7881-400e-ae70-2f96519e530b%2Fb1ec025a-8a75-41e8-bdf0-b33079167bae%2Ff8obdn6_processed.jpeg&w=3840&q=75)
Transcribed Image Text:## Educational Website Content
### Analysis of Variance (ANOVA) Problem
**Problem Statement:**
Let \( \mu_1, \mu_2, \mu_3, \mu_4 \) be the means of four normal distributions with a common, but unknown, variance, \( \sigma^2 \). To test, at the \(\alpha = 0.01\) significance level, the hypothesis:
\[ H_0 : \mu_1 = \mu_2 = \mu_3 = \mu_4 \]
We take a random sample of size five from each of these distributions. Determine whether \( H_0 \) should be accepted or rejected, using the following observed sample values:
**Observed Sample Values:**
- Distribution 1: 12, 16, 19, 23, 10
- Distribution 2: 16, 11, 20, 15, 13
- Distribution 3: 25, 21, 19, 29, 26
- Distribution 4: 22, 19, 28, 24, 31
### Tasks:
**A) Show the entire ANOVA table.**
Construct an ANOVA table that includes the sources of variation, sum of squares, degrees of freedom, mean squares, and the F-ratio.
**B) Identify the Critical Region**
Determine the critical region based on the F-distribution with the appropriate degrees of freedom and significance level (\(\alpha = 0.01\)).
**C) Decision for the Hypothesis Test**
Make a decision for the hypothesis test. Should the null hypothesis \( H_0 \) be accepted or rejected? Justify your decision based on the calculated F-ratio and the critical value.
### Additional Information:
- **Diagram** or **Graph Explanation**: No diagrams or graphs are present in the problem.
- Use statistical software or manual calculations to complete the ANOVA table and hypothesis test.
- Make sure to verify calculations for accuracy, as the problem stems from a typical scenario in statistics involving hypothesis testing using ANOVA.
This problem helps in understanding the application of ANOVA in testing the equality of means from multiple groups with a given statistical significance level.
Expert Solution
Step 1
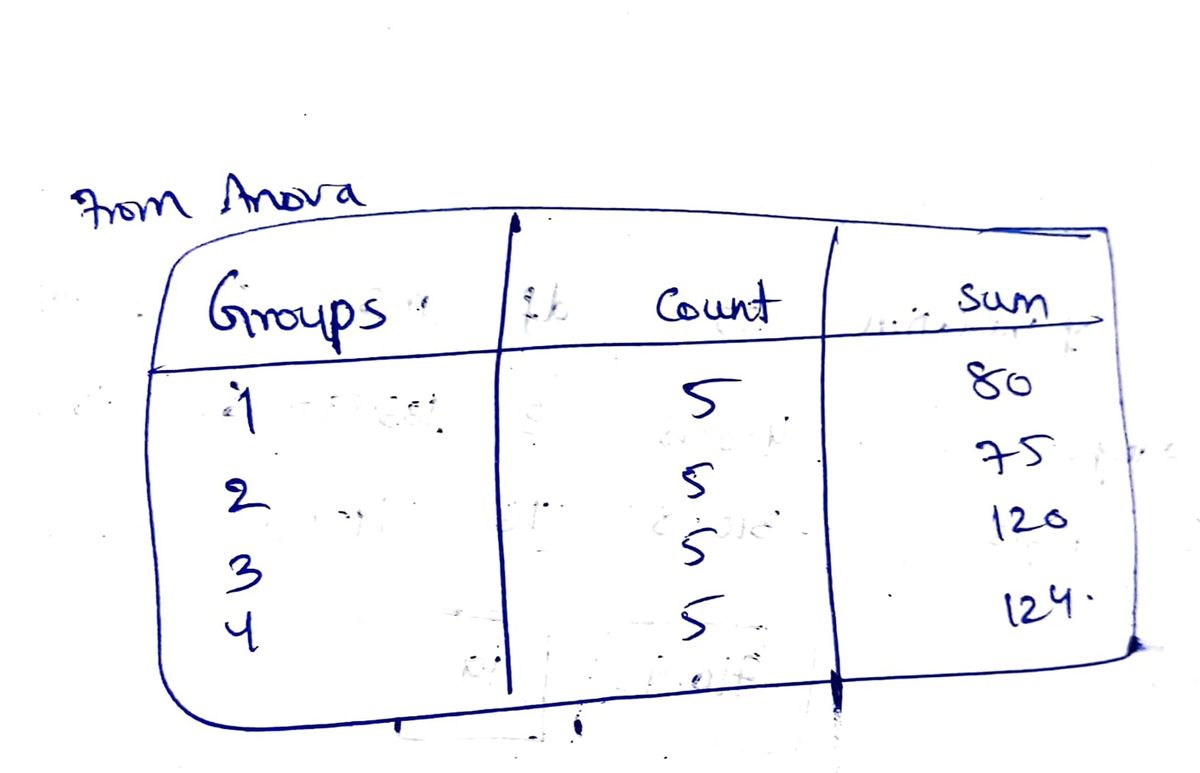
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman