Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
Find the volume of the solid bounded by the graphs of the given equations (given in cylindrical coordinates).
r2 + z2 = a2 and r = a(cos(theta))
a=4
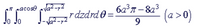
Transcribed Image Text:6a?7 -8a3
(a>0)
I cacose aVa2-7
rdzdrd0 =.
9
Transcribed Image Text:4.5
umber 7
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- The motion of a fluid particle is defined parametrically as follows,x(t) = sinh(t), and y(t) = cosh(t). Show that [please see image]arrow_forwardUse spherical coordinates to evaluate (2²+² +2²) ¹/4 dV, where E is the solid E 2 that lies between x² + y² +2²=1 and 2 2 x² + y² +²=4 given in the figure. 2 ZA x² + y² + z² = 4 x² + y² +2²=1arrow_forwardPart 3). Consider the right triangle shown below. Verify that y h by using calculus principles to solve the centroid using O as the reference point. [HINT: If A = x*y, then dA = dx*y or dA =x*dy.]arrow_forward
- Therefore, the system in polar coordinates given by i = r(1 – r2 – r² sin? 20) 0 = 1+ 4r? cos 0 sin 0. c) Determine the circle of maximum radius, r1, centered on the origin such that all trajectories have a radially outward component on it.arrow_forwardThe following points are given in cylindrical coordinates; express each in rectangular coordinates and spherical coordinates. Cylindrical (r, 0, z) (1, 45°, 9) (3, 1,-4)|( 2 (0, 45°, 9) (5,, 12) ( 6 (1,2,0) 3π 4 -1 -6 Rectangular (x, y, z) DIC DIC DIC DIC DIC DIC Spherical (ρ, θ, φ) Crookarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,