Question
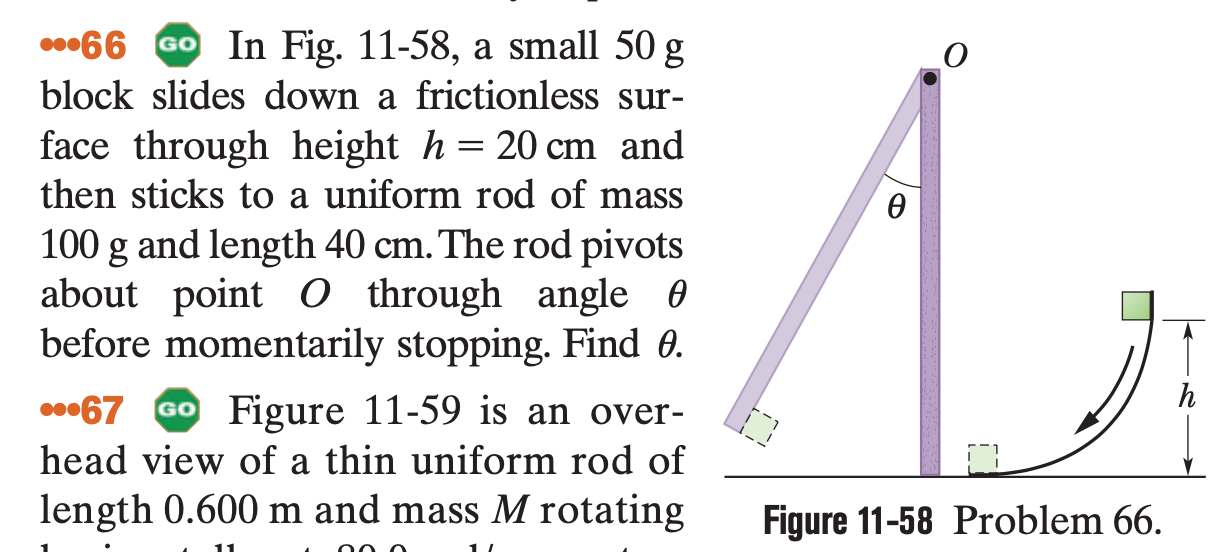
Transcribed Image Text:•66 GO In Fig. 11-58, a small 50 g
block slides down a frictionless sur-
face through height h = 20 cm and
then sticks to a uniform rod of mass
Ө
100 g and length 40 cm. The rod pivots
about point 0 t hrough angle 0
before momentarily stopping. Find 0.
67
GO Figure 11-59 is an over-
head view of a thin uniform rod of
length 0.600 m and mass M rotating
Figure 11-58 Problem 66.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Similar questions
- 5) A disk of mass m = 75.0 g and radius r = 4.20 cm glides across an air table at a speed v = 1.5 m/s. It makes a glancing collision with a hoop of radius R = 5.80 cm and mass M = 130 g (initially at rest) such that their rims just touch. Because their rims are coated with instant-acting glue, the two objects stick together and rotate after the collision. a) What is the angular momentum of the system relative to the center of mass? b) What is the angular speed about the center of mass?arrow_forward7) A non-rotating uniform hoop of radius kb and mass m is dropped onto a rotating uniform disk of radius b and mass 3m. If the disk is initially rotating with angular velocity @,, what is w, after friction makes two objects rotate with the same angular velocity? Assume the central axes of both objects always lie exactly along the same axis of rotation. XA) @, =0, B) @, = 0, C) @, =0, General c.o.m. Moments MR? I hoop of mass M, radius R %3D Dinsction Idisk of =MR force mass M radius R E) Зт, о,arrow_forward77. . A uniform, solid sphere of radius 5.00 cm and mass 3.00 kg starts with a translational speed of 2.00 m/s at the top of an inclined plane that is 2.00 m long and tilted at an angle of 25.0° with the horizontal and rolls without slipping down the ramp. What is the sphere's speed at the bottom of the ramp? Example 9-13arrow_forward
- Problem A) At a circus you see a man spinning plates with radii of 75 cm on top of long poles. The plates have a constant angular acceleration of 0.6 rad/s?. Assuming the plates start from rest, after a time of 8 seconds calculate a) how many revolutions they have made, b) their angular velocity, c) their tangential acceleration, d) their radial acceleration, and e) their overall acceleration, magnitude and direction with respect to the edge of the disk.arrow_forwardA baseball has a mass of 0.15 kg and radius 3.7 cm. In a baseball game, a pitcher throws the ball with a substantial spin so that it moves with an angular speed of 37 rad/s and a linear speed of 51 m/s Assuming the baseball to be a uniform solid sphere, determine the rotational and translational kinetic energies of the ball in joules. КЕ Frotational KEtranslationalarrow_forwardA cylindrical bar with a sphere firmly attached to one end is originally at rest in a horizontal position. The bar is pivoted about a free hinge at one end (Figure 8-61). The bar is 4.00 m long and has a mass of 231 kg. The sphere has a radius of 60.0 cm and a mass of 53.0 kg. A variable torque is applied to lift the bar by rotating it 37.0° about the pivot at a constant angular speed. Calculate the work done by the variable torque.arrow_forward
- The moment of inertia of an object about a certain axis is 1.2 kg-m2. Initially the object is at rest, and then it is accelerated at a constant rate of 25 rad-s-2. Determine the time required for the object to achieve a rotational kinetic energy of 1.50 kJ.arrow_forwardA uniform solid sphere of mass 12.0 kg and radius 7.0 cm rotates at 300 revolutions per minute (rpm) on an axis passing through its center. Calculate: a) Its moment of inertia b) Its rotational kinetic energy c) The angular momentum (L), that is, the magnitude of the product Iw, in the appropriate IS units d) Based on the general definition of the moment of inertia (I = Mr²), determine the radius of gyration of the sphere around the axis that passes through its center.arrow_forwardA uniform solid disk of mass m = 2.99 kg and radius r = 0.200 m rotates about a fixed axis perpendicular to its face with angular frequency 6.05 rad/s. (a) Calculate the magnitude of the angular momentum of the disk when the axis of rotation passes through its center of mass. kg • m2/s (b) What is the magnitude of the angular momentum when the axis of rotation passes through a point midway between the center and the rim? kg • m2/sarrow_forward
arrow_back_ios
arrow_forward_ios