
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
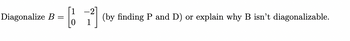
Transcribed Image Text:**Problem: Diagonalize the Matrix B**
Given the matrix \( B = \begin{bmatrix} 1 & -2 \\ 0 & 1 \end{bmatrix} \), our objective is to either:
1. Find matrices \( P \) and \( D \) such that \( B = PDP^{-1} \), where \( D \) is a diagonal matrix, and \( P \) is an invertible matrix, or
2. Explain why \( B \) is not diagonalizable.
To find \( P \) and \( D \):
- **Step 1**: Calculate the eigenvalues of matrix \( B \).
- **Step 2**: Determine the eigenvectors corresponding to each eigenvalue.
- **Step 3**: Form matrix \( P \) using the eigenvectors as its columns.
- **Step 4**: Construct the diagonal matrix \( D \) with the eigenvalues on its main diagonal.
If there aren't enough linearly independent eigenvectors to form \( P \), then matrix \( B \) is not diagonalizable.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- How would I find the basis and range rank for this linear algebra question?arrow_forward• A is in RREF ● -689 Let A Fill in the blanks such that A has all of the following properties. row(A) is the xz-plane. null(A) is the y-axis. It follows that im(A) is thearrow_forwardFind the cross product a × b. = (t, t², t³), a b = (1, 4t, 9t²)arrow_forward
- Consider below presented polynomials v1, v2, v3, v4in P2. v1 = 2t2 + t + 2 v2 =t2 - 2t v3 =5t2 – 5t + 2 v4 =-t2 - 3t – 2 Determine whether the vector v = t2 + t + 2 belong to span {v1, v2, v3, v4}or not.arrow_forward4 VI V2 = 3 V3 = V4 Write w as a linear combination of v ,..., V4 in two different ways. Don't leave any fields blank. Use the coefficient O if you don't need one of the vectors. First answer: w = V + V2 + V3 Second answer: %3= VI + V2 + V3 + V4 .arrow_forwardLet A = [1 -1 -1 -1 1 -1 -1 -1 1]. Find a diagonalization if possible.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

