Question
Transcribed Image Text:Solution HW1Q5-by: write your full name here
Page 10
Page 10 of 18
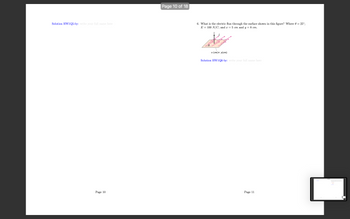
= 25°;
6. What is the electric flux through the surface shown in this figure? Where 0 =
E = 100 N/C; and x = 5 cm and y = 8 cm.
n
E
x (cm) x y(cm)
Solution HW1Q6-by: write your full name here
Page 11
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- What is the net electric flux through each of the four surfaces shown in the figure below? (Assume Q1 = 38.5 µC and Q277.0 μC.) ФЕ,1 %3 N. m?/C DE,2 = N. m?/C ФЕ,З N. m?/c %3D ФЕ 4 N. m?/C + +Qarrow_forward07 A closed surface with dimensions a = b = 0.400 m and c = 0.800 m is located as shown in the figure below. The left edge of the closed surface is located at position x = a. The electric field throughout the region is non- uniform and given by E. = [k (xy?) ↑ + k (x²y)j] N/C, where x,y are in meters, k =5.00 m3 1) Use ( E · îdA to calculate the flux through each surface. (should be SIX answers)arrow_forwardFind the electric flux through the closed surface whose cross-section is shown below. a a -2.0 × 10-6 C a. -2.00 × 10-N·m²/C O b. -2.00 × 10-6a² N·m²/C -2.25 × 105 N·m²/C c. d. -2.25 × 105a² N·m²/Carrow_forward
- 5. A thick, conducting, metal shell of inner radius R1 = 0.5m and outer radius R2 = 1.5m has a net charge of (-10C). Also, a (-3C) point charge is at the origin (center). Find the surface charge density on the inner surface of the shell. 6. Same setup as problem 5. Find the magnitude of the electric field at 4 meters from the center of the shell. 7. Same setup as problem 5. Find the magnitude of the electric field at 1.1 meters from the center of the shell.arrow_forward3. A very long wire contains a uniform negative charge density -A. A charge -q rests inside a spherical Gaussian surface of radius R. The sphere's center lies on the wire. Located outside the sphere is another charge +q. What is the total electric flux through the sphere? -2 (a) D = k (2 +q ) / ɛo (b) 0 = -q / ɛ0 (c) 0 = -k q / R? R (d) 0 = 0 (e) O = (-2 2R-q) / ɛo Gaussian Surfacearrow_forwardA closed surface is in the form of a block with length c, width b and height a. In this room there is an electric field parallel to the x axis with magnitude: E = A + Bx, where A and B are constants. a. Determine the total flux over the closed surface. b. Determine the amount of charge covered by the payload. N x = a ko-arrow_forward
arrow_back_ios
arrow_forward_ios