
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
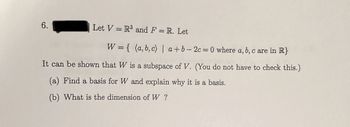
Transcribed Image Text:6.
Let V = R³ and F = R. Let
W = { (a,b,c) | a+b=2c=0 where a, b, c are in R}
It can be shown that W is a subspace of V. (You do not have to check this.)
(a) Find a basis for W and explain why it is a basis.
(b) What is the dimension of W?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- Really need help with steps so I may understandarrow_forwardSpent a lot of time solving it, need some helparrow_forwardGiven basis B = {(1, -1), (2, 3)} and basis C = {(1, 0), (0, 1)}, and linear map T = (x + 2y ; 2x - y) from R2 --> R2, find the coordinate vectors of basis C in terms of basis B.arrow_forward
- a b 6. Let H be a subspace of M2x2 whose vectors are of the form Then, B с 0 is a basis for H. 10 Find the coordinate vector of v = according to the basis, B.arrow_forwardQ7: Find a basis for the following vector spaces. a (a) V = 4b — За — d (b) W a-4e = 86+3d 2e = darrow_forwardFind a basis for the plane 4x + 3y + 5z = 0 in R³. |arrow_forward
- 4 Let W = span(vV1, V2) where vi = and v2 2 . Then: (a) Find the orthogonal decomposition of the vector x = 3 (b) Find an orthogonal basis for W- (remember to justify your answer).arrow_forwardLet w,=(1,0,0,1) and w=(-1,0,0,1). Let W=(w | w w, = w-w, = 0}, where w-w, denotes the dot product of w, & w. (a) Show that W is a vector space (over the field R). (b) Find the basis of W. (c) Find the dimension of W. (d) Is the answer to part (c) unique?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

