Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: fOo)=Sinx-41 Cos x 1X-1 cos X (x)
A:
Q: Find the exact value of the expression in the terms of x cos(sin- ()) '25-(ӕ—2)2 V8+(z-30)2 125…
A: Inverse Trigonometry
Q: Verify the identity: sin²x (1+ncot²x) + cos²x (1+tan²x) = sin²x(n+cot²x) + cos²x(n+tan²x)
A:
Q: I'm having trouble trying to solve the problem csc x - csc x cos2 x = sin x. I'm having trouble…
A: you will need to use only these identities to solve the question;
Q: Show that the equation 2x + cos(x) = 1 has exactly one root. (IVT and Rolle's Theorem)
A:
Q: sin' t – cos' t Prove tan?t – 1 cos? t
A:
Q: Evaluate: Scos 2xdx cos2x, cos 2x +C A 2 6 sin2x sin32x +C 6. B 2 cos2x cos 2x + C 6. 2 sin2x,…
A:
Q: Prove that sin? 0 + cosª 0 = sin“ 0 + cos² 0.
A: Using fundamental identity of trigonometry.
Question
**Problem 6: Prove the Trigonometric Identity** Prove that: \[ \cos^4 x - \sin^4 x = \cos 2x \] This is a trigonometric identity that demonstrates the relationship between the fourth powers of sine and cosine functions and the double angle cosine. To prove this identity, utilize trigonometric identities and algebraic manipulation. **Solution Outline:** 1. Start with the left side of the equation, \( \cos^4 x - \sin^4 x \). 2. Use the difference of squares identity: \[ a^2 - b^2 = (a - b)(a + b) \] Thus, express \( \cos^4 x - \sin^4 x \) as: \[ (\cos^2 x - \sin^2 x)(\cos^2 x + \sin^2 x) \] 3. Recall the Pythagorean identity: \[ \cos^2 x + \sin^2 x = 1 \] Substitute this into the expression: \[ (\cos^2 x - \sin^2 x)(1) = \cos^2 x - \sin^2 x \] 4. Use the double angle identity for cosine: \[ \cos 2x = \cos^2 x - \sin^2 x \] Conclude that: \[ \cos^4 x - \sin^4 x = \cos 2x \] This demonstrates the correctness of the identity through algebraic manipulation and application of known trigonometric identities.
expand button
Transcribed Image Text:**Problem 6: Prove the Trigonometric Identity** Prove that: \[ \cos^4 x - \sin^4 x = \cos 2x \] This is a trigonometric identity that demonstrates the relationship between the fourth powers of sine and cosine functions and the double angle cosine. To prove this identity, utilize trigonometric identities and algebraic manipulation. **Solution Outline:** 1. Start with the left side of the equation, \( \cos^4 x - \sin^4 x \). 2. Use the difference of squares identity: \[ a^2 - b^2 = (a - b)(a + b) \] Thus, express \( \cos^4 x - \sin^4 x \) as: \[ (\cos^2 x - \sin^2 x)(\cos^2 x + \sin^2 x) \] 3. Recall the Pythagorean identity: \[ \cos^2 x + \sin^2 x = 1 \] Substitute this into the expression: \[ (\cos^2 x - \sin^2 x)(1) = \cos^2 x - \sin^2 x \] 4. Use the double angle identity for cosine: \[ \cos 2x = \cos^2 x - \sin^2 x \] Conclude that: \[ \cos^4 x - \sin^4 x = \cos 2x \] This demonstrates the correctness of the identity through algebraic manipulation and application of known trigonometric identities.
Expert Solution
Check Mark
Step 1

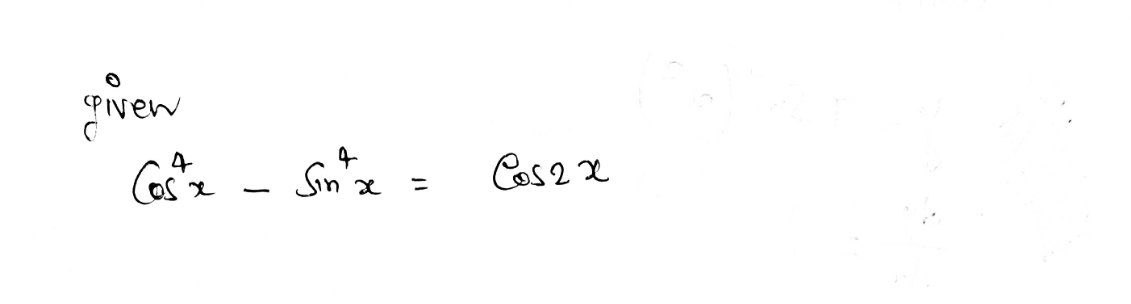
Calculus homework question answer, step 1, image 1

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS