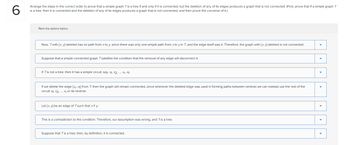
6 Arrange the steps in the correct order to prove that a simple graph T is a tree if and only if it is connected, but the deletion of any of its edges produces a graph that is not connected. (First, prove that if a simple graph 7 is a tree, then it is connected and the deletion of any of its edges produces a graph that is not connected, and then prove the converse of it.) Rank the options below. Now, Twith {x,y) deleted has no path from x to y, since there was only one simple path from x to y in T, and the edge itself was it. Therefore, the graph with (x, y) deleted is not connected. Suppose that a simple connected graph 7 satisfies the condition that the removal of any edge will disconnect it. If T is not a tree, then it has a simple circuit, say, x1, x2. X. xq. If we delete the edge (x₁, x₁) from T, then the graph will remain connected, since wherever the deleted edge was used in forming paths between vertices we can instead use the rest of the circuit x1, x2. .x, or its reverse. Let (x, y) be an edge of Tsuch that x# y. This is a contradiction to the condition. Therefore, our assumption was wrong, and T is a tree. Suppose that T is a tree; then, by definition, it is connected. ▾

2. Draw a parsing tree for a. (8x – y)5 – 7/4z – 3. b. (a – (3+2b))/(c² + d). - - -

question c Direct proof/proof by cases:

Consider the tree diagram. Path number 1 B1 C2 2 4 C2 4 4 4 B3 6 3 Find P(C,|B2) · P(B2). (Enter your answer as a fraction.)

Which of the following graphs contain a subdivision of K3,3 as a subgraph

Show all possible connected sub graphs of the following graph. How many of them are there refer to image below

Let G be the graph below. The edges are labeled by integers. a 1 10 b 8 = /20 19 2 J C 12 13 If 18 g 17 3 7 d 14 15 h 16 k 4 6 e UT l 1. List the edges of the spanning tree of G obtained by the breadth-first search with the vertex ordering a, b, c, . . . , l. (The answer should be a list of integers (edge labels). The order in the list does not matter.) 2. List the edges of the spanning tree of G obtained by the depth-first search with the vertex ordering a, b, c, ..., l.

Refer to the accompanying graph. Complete parts (a) through (c) in order. Starting at A, the circuit is Starting at B, the circuit is Starting at C, the circuit is Starting at D, the circuit is Starting at E, the circuit is (Simplify your answers.) (b) Which of the circuits for M A. The circuit that stai TL-- AL - and the total weight is otal weight is otal weight is otal weight is otal weight is A D C E→B→A A B C D→E→A A C D E→B→A ... A-E→C D→B→A B 13 15 60 C (a) Use the nearest neighbor algorithm starting at each of the vertices in turn to determine an approximate solution to the problem of finding a minimum Hamilton circuit for the graph. In each case, find the total weight of the circuit. 6/ 57 14 9 8 E 12 D ion to the problem of finding a minimum Hamilton circuit for the graph? Select all that apply.