
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
please help me answer questions 6 and 14
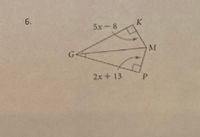
Transcribed Image Text:### Geometry Problem 6
The diagram presents a geometric figure consisting of two adjacent right triangles, labeled \( \triangle GMK \) and \( \triangle GMP \). Both triangles share the vertex \( G \) and the side \( GM \).
- **Vertices**: The vertices of the figure are labeled as \( G \), \( K \), \( M \), and \( P \).
- **Angles**:
- The angle at vertex \( M \) in \( \triangle GMK \) is a right angle (90 degrees), and is marked with a small square.
- Similarly, the angle at vertex \( M \) in \( \triangle GMP \) is also a right angle (90 degrees), indicated by a small square.
- **Angle Measures**:
- The external angle at vertex \( G \) between sides \( GK \) and \( GM \) is labeled \( 5x - 8 \).
- The external angle at vertex \( G \) between sides \( GM \) and \( GP \) is labeled \( 2x + 13 \).
This geometric representation is commonly used to illustrate the concepts of right angle triangles, angle relationships, and can be used in problems involving algebraic expressions and geometric properties.
For analysis:
- Consider the relationships between the angles in adjacent triangles and the properties of right triangles.
- Utilize algebraic methods to solve for the variable \( x \) if needed.
Note: Ensure that the sum of the angles around point \( G \) equals \( 360^\circ \), a fundamental property in planar geometry.
![### Problem 14.
**Given:**
An isosceles triangle is shown with the two equal sides marked with a short line each. The angles opposite those sides are marked as \( x^\circ \) (at the top vertex) and \( y^\circ \) (at the bottom right vertex). The angle at the bottom left vertex is given as \( 43^\circ \).
**Find:**
Values of \( x \) and \( y \).
**Solution:**
1. In an isosceles triangle, the angles opposite to the equal sides are also equal. Hence, \( x = y \).
2. The sum of all interior angles in any triangle is always \( 180^\circ \).
Therefore:
\[
x + y + 43^\circ = 180^\circ
\]
3. Since \( x = y \):
\[
x + x + 43^\circ = 180^\circ
\]
\[
2x + 43^\circ = 180^\circ
\]
4. Solving for \( x \):
\[
2x = 180^\circ - 43^\circ
\]
\[
2x = 137^\circ
\]
\[
x = \frac{137^\circ}{2}
\]
\[
x = 68.5^\circ
\]
5. Since \( x = y \):
\[
y = 68.5^\circ
\]
**Conclusion:**
\[
x = 68.5^\circ \quad y = 68.5^\circ
\]
**Answer:**
\[
x = 68.5^\circ \quad y = 68.5^\circ
\]](https://content.bartleby.com/qna-images/question/b0806c0e-0103-48e4-89cd-443bacc85606/2a32ff08-d7ee-4a7c-a6e3-562e2774cebd/52u8goq_thumbnail.jpeg)
Transcribed Image Text:### Problem 14.
**Given:**
An isosceles triangle is shown with the two equal sides marked with a short line each. The angles opposite those sides are marked as \( x^\circ \) (at the top vertex) and \( y^\circ \) (at the bottom right vertex). The angle at the bottom left vertex is given as \( 43^\circ \).
**Find:**
Values of \( x \) and \( y \).
**Solution:**
1. In an isosceles triangle, the angles opposite to the equal sides are also equal. Hence, \( x = y \).
2. The sum of all interior angles in any triangle is always \( 180^\circ \).
Therefore:
\[
x + y + 43^\circ = 180^\circ
\]
3. Since \( x = y \):
\[
x + x + 43^\circ = 180^\circ
\]
\[
2x + 43^\circ = 180^\circ
\]
4. Solving for \( x \):
\[
2x = 180^\circ - 43^\circ
\]
\[
2x = 137^\circ
\]
\[
x = \frac{137^\circ}{2}
\]
\[
x = 68.5^\circ
\]
5. Since \( x = y \):
\[
y = 68.5^\circ
\]
**Conclusion:**
\[
x = 68.5^\circ \quad y = 68.5^\circ
\]
**Answer:**
\[
x = 68.5^\circ \quad y = 68.5^\circ
\]
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning