
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
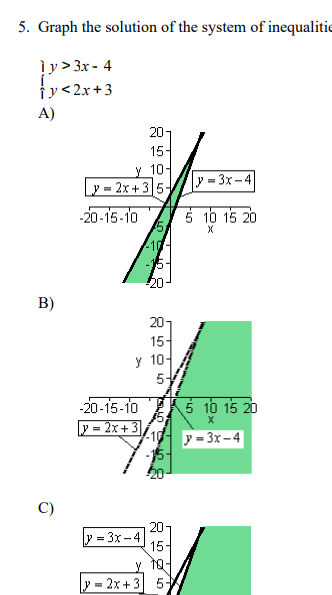
Transcribed Image Text:**Graphing the Solution of a System of Inequalities**
**Problem Statement:**
Graph the solution of the system of inequalities:
1. \( y > 3x - 4 \)
2. \( y < 2x + 3 \)
**Graph Representations:**
**A. Graph Details:**
- The graph includes two lines, \( y = 3x - 4 \) and \( y = 2x + 3 \).
- The line \( y = 3x - 4 \) is solid, indicating that the solution may not include the values on this line.
- The line \( y = 2x + 3 \) is solid as well, indicating that the solution might not include the line itself.
- The region of interest (potential solution) does not seem to be shaded in this portion, and hence doesn't show the correct solution set.
**B. Graph Details:**
- Shows the same two lines, \( y = 3x - 4 \) and \( y = 2x + 3 \).
- The line \( y = 3x - 4 \) is dashed, indicating values on this line are not included in the solution.
- The area that may satisfy both inequalities is shaded in green.
- The shading represents the region where the inequality \( y > 3x - 4 \) and \( y < 2x + 3 \) both hold true.
**C. Graph Details:**
- Similar to the previous graphs with the lines \( y = 3x - 4 \) and \( y = 2x + 3 \).
- The method of diagramming and shading might differ from B, while still aiming to identify the overlapping region where both inequalities are satisfied.
- It does not clearly represent the correct solution if shading is inconsistent with the given inequalities.
**Graph Interpretation:**
- In graph B, the shading correctly represents the solution region where both inequalities \( y > 3x - 4 \) and \( y < 2x + 3 \) are simultaneously satisfied.
- In checking solutions for systems of inequalities, look for regions where required shading overlaps, with attention to line types (dashed or solid) denoting inclusion or exclusion of boundary lines.
Expert Solution
arrow_forward
Step 1
y is greater then f(x) then, area is upper size
If less then, area is lower side
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Hi can I please get some assiatance with this problem, I'm a bit stuck on the steps. Thank you.arrow_forward6. Find the value(s) of h so that the linear system 6b) * xi +3x2 = -1 is inconsistent. 5x1 + hx2 =7arrow_forwardSketch the solution to each system of inequalities. 1) ys-x- 2 y2 -5x +2 2) y>-x - 2 y<-5x + 2 3), ys*+2 4) xs-3 5 y<-x+2 y<-2x – 3arrow_forward
- What is the solution to the system of equations represented in the graph? I got 4 diffrent answers and im now sure what it is would it be (5, 10)? (5, 11)? (6, 10)? (6,11)?arrow_forwardWhich system of equations would result in the elimination of the x-value? a) 3(2x+5y=15) -2(3x+4y=19) b) 4(2x+5y=15) -5(3x+4y=19) c) -3(2x+5y=15) -2(3x+4y=19) d) -4(2x+5y=15) -5(3x+4y=19)arrow_forwardWhat is the graph of the system y = -2x + 3 and 2x + 4y = -8? aa -E -1. --4 -0 -1. **arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

