5. G (a + b.2: a eZ and b e Z) is a group under addition in the reals.Define o : G -→G for all a + b.2 e G, as 0(a+ b.2) = a- b./2. Provethat o is an automorphism.

Answered: Image /qna-images/answer/f7be9a1b-0963-4f4b-aeaf-d975c187ccbe.jpg

Answered: 5. G = {a + b2: a eZ and be Z) is a…

5. G = {a + b2: a eZ and be Z) is a group under addition in the reals. Define o: G G for all a+ b./2 eG, as (a+ b /2) = a- b./2. Prove that o is an automorphism.

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Related questions

Q: on G by a * b = ba. Prove that G is isomorphic

Q: Suppose that g and h induce the same inner automorphism of a group G. Prove that h-'g E Z(G).

A: Given: g , h induce the same inner automorphism of a group G. Prove that: h-1g∈ZG.

Q: Suppose F1 and F2 are distinct reflections in a dihedral group Dn.Prove that F1F2 ≠ R0.

A: Given: F1 and F2 are distinct reflections in a dihedral group Dn. To Prove: F1F2≠R0.

Q: 2. Let G = (R*, .), the multiplicative group of nonzero real numbers. Let H = {x ER: x -1} be the…

A: 2. Let , the multiplicative group of non-zero real numbers.Let be the group with operation .Prove…

Q: If (G,X) be the group of all real 2 x 2 matrices (b) such that ad - bc #0 with matrix multiplication…

A: Given if G, × be the group of all 2×2 matrices abcd such that ad - dc≠0 with matrix multiplication…

Q: Let R* be the group of nonzero real numbers under multiplication,and let r be a positive integer.…

A: Given: R* is the group of nonzero real numbers and r is a positive integer.We need to show that the…

Q: 8. u(0,1)= 0, u(1, 1) = 0, t>0 u(x, 0) = 4 sin 3x + 8 sin 6mx, 0<x<1

Q: Let R = R \ {-1} and define the operation ♡ on R by a♡b = ab + a + b Va, b E R. Show that (a) ♡ is a…

Q: 1. Let A be an abelian group, and let G = A × A (Cartesian product), which also is a group. Let 6:…

Q: Define on S = Q × Q* the operation (a, b) * (x, y) = (ay+ x, by). Recall that Q* = Q\{0}. 1. Explain…

Q: Show that Z12 is not isomorphic to Z2 ⊕ Z6. Recall that ℤ? denotes the abelian cyclic group of order…

A: It has to be proved that Z12 is not isomorphic to Z2 ⊕ Z6. Isomorphism is defined as one-to-one…

Q: 6. Show the ring {a+bv2|z, b € Z} has exactly 2 automorphisms. These are the identity and the map…

Q: What is the automorphism group of ?A ut (Z3, +)

A: Thanks for the question :)And your upvote will be really appreciable ;)

Q: Let R" = {(a,, a, . .. , a) l a, E R}. Show that the mapping o: (a,, Az, ... , a) → (-q,, -a, · .…

A: Given: ℝn=a1.....,anai∈ℝWe need to show that the mapping ϕa1,.....,an→-a1,.....,-an is an…

Q: 22, Use mathematical induction to prove that if a1, a2, ... , an are elements of a group G, then…

A: See the detailed solution below.

Q: 5. Define the right regular action of a group G on itself. Show it is a group action. Is it…

Q: Suppose that f: XY is a homomorphism (of either groups or rings). Prove that f is injective if and…

Q: Let G be an Abelian group. Determine all homomorphisms fromS3 to G.

A: Given: G is an Abelian group.To find: All homomorphisms from S3→G.

Q: 2. If a is an involution, then Baß is an involution for any transformation B.

A: It is given that α is an involution. So, we can say that α2=I.

Q: Show that the mapping f: Z (VZ)→Z(VZ) defined by f(a + bV2) = a – bv2 is an automorphism on the ring…

Q: Prove that G = {a+b√2: a, b € Q and a and b are not both zero} is a subgroup of R* under the group…

A: Given- G=a+b2: a,b∈ℚ and a and b are not both zero To prove- G is a subgroup of ℝ* under the group…

Q: Let f. → (R, +> be defined by f(x) = 3x- 3 Prove or disprove that f is an isomorphism from the…

A: This is related to isomorphism

Q: and m' be two R-modules. e set Hom, CM, Mm) is an group under pointwise of morphism

Q: 1. Let (G, +) and (H,*) be groups. The direct product of G and H is the set G × H equipped with…

Q: Let f be the homomorphism f Z15 GL(2) of groups such that (1)-A, where A- a) Give the definition of…

Q: Let (G, ★) and (G,o) be groups, with respective identity elements e and ē. Suppose there is a…

Q: 1. Explain the relations between a group (G,+), a ring (R,+,.) and an R-module over a ring R. 2 Name…

A: Group (G,+)A group is a set G equipped with a single binary operation +(called addition) that…

Q: Find a matrix M such that M-¹0 (8) M = (19) for every element g € S3. Conclude that the…

Q: If G is an abelian group, prove that (a * b)" = a" * b" for all integers n.

A: Given: "G" is an abelian group, We need to prove that a×bn=an×bn for all integers n. Abelian Group…

Q: Let f: - be defined by f(x) = 3x-3. Prove or disprove that f is an isomorphism from the additive…

A: Consider the given information: Let f:ℝ,+→(ℝ,+) be defined by, f(x) =3x-3 To find that f is an…

Q: Let R be a ring and f: R → R be defined by f(x) = x³. Check All that are correct. fis onto when R =…

A: According to experts guidelines of bartleby i have to solve first three parts of the problem. So…

Q: Find an isomorphism o from the multiplicative group G of nonzero complex numbers to the…

A: We need to find ϕ for the multiplicative group G of non zero complex numbers to the multiplicative…

Q: 2. Let U be a ring with unity 1 and zero element 0.. (a) If 0 = 1, then U consists of only one…

Q: Show that any automorphism of GF( pn) acts as the identity onGF( p).

Q: Let G =U (7)OZ, . The order of G is O 7 О 35 О 1 30

A: In U(n) which unitary group of order n, if n is prime number that group order will be n-1. Here in…

Q: Let G1 and G2 be groups. Prove that G1 × G2 is isomorphic to G2 × G1.

Q: Let S = R\{-1}. Define * on S by a * b = a+b+ ab. Prove that (S, *) is an abelian group.

Q: Determine whether an onto homomorphism between the groups D6 and D3 + Z2 exists.

Question

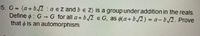
5. G (a + b.2: a eZ and b e Z) is a group under addition in the reals.
Define o : G -→G for all a + b.2 e G, as 0(a+ b.2) = a- b./2. Prove
that o is an automorphism.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step 3

VIEW

Step by step

Solved in 3 steps with 3 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Groups$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions

Let S = {x ER| x + 3}. Define * on S by a * b = 12 - 3a - 3b + ab Prove that (S, *) is a group.
Consider 2-element group {} where + is the identity. Show that the map RX → {±} sending a to its sign is a homomorphism. Compute the kernel.
Decide if the abelian group Z/2 × Z/2 is cyclic or not. Prove your answer
Show that for distinct i and j from {1,...n} there are exactly two auto- morphisms of Cn which send i to j. Then Show that there are exactly 2n automorphisms of Cn.
8. Let the set G ZXZ and the binary operation on G be given by the rule (a, 6) • (c, d) = (a + r, 6+ d). It is easily verified that the pair (G, ) is a commutative group. a) Show that the mapping f: G- Z defined by fl(a, b)] = a is a homomorphism from (G, ) onto the group (2,+). b) Determine the kernel of this mapping. c) If II = {(a, a) | a E Z}, prove that (H, ) is a subgroup of (G, ), which is isomorphic to (Z,+) under the function f.
Show that the mapping Φ(a + bi) = a - bi is an automorphism of the group of complex numbers under addition. Show that Φ preserves complex multiplication as well—that is, Φ(xy) = Φ(x)Φ(y)
Let (IR,+) be a group of real numbers under addition and (R+,-) be the group of positive real numbers under multiplication. Prove f: R→ R+ by f (x)= ex for all x ER is homomorphism and isomorphism.
Let G and H be groups and o : G → H be a homomorphism. c. Define the maps n1 : G x H → G and 72 : G x H → H by 1(9, h) = g and 72(9, h) = h respectively. %3D Show that 71 and n2 are homomorphisms and find their kernels.
6. Additional Classifications: Classify the factor group according to the fundamental theorem of finitely generated abelian groups: a. (Z₁ × Z₁2)/((3,6)) b. (Z x Z)/((3,6))
I need help with #4.20
If ring (R1, +, *) is isomorphic to ring (R2, +, *) with f being the isomorphism,then prove the following statements:a. f(e1) = e2, where e1 is the identity element for the group (R1, +) and e2 isthe identity element of the group (R2, +).b. f(-a) = -f(a), for each element ‘a’ in R1, where –a represent the additiveinverse of element ‘a’ in R1 and –f(a) represents the additive inverse of theelement f(a) in R2.c. If (R1, +, *) is a ring with (multiplicative) identity I1 and (R2, +, *) is a ringwith (multiplicative) identity I2, then f(I1) = I2.
Determine the group of field automorphisms of GF(4).