
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
thumb_up100%
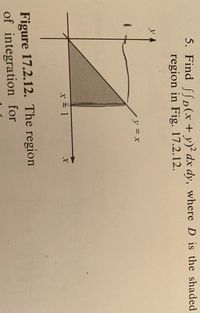
Transcribed Image Text:**Problem 5:**
Find \(\iint_D (x+y)^2 \, dx \, dy\), where \(D\) is the shaded region in Fig. 17.2.12.
**Details of Figure 17.2.12:**
The figure illustrates a Cartesian coordinate system with a shaded triangular region. The boundaries of the region are:
- The line \(y = x\).
- The line \(x = 1\).
- The x-axis (\(y = 0\)).
The region is bounded as follows:
- From \(x = 0\) to \(x = 1\).
- The region is above the x-axis and below the line \(y = x\).
**Graph Explanation:**
- The x-axis is horizontal, and the y-axis is vertical, meeting at the origin \((0,0)\).
- The line \(y = x\) begins from the origin at a 45-degree angle, extending diagonally upwards to the right.
- The line \(x = 1\) is vertical, intersecting the x-axis at \(x = 1\).
- The shaded region is a right triangle with vertices at \((0,0)\), \((1,0)\), and \((1,1)\).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Similar questions
- Find the Gini index of income concentration for the Lorenz curve with the following equation. 1 y= 2x/2+2x Table of Integrals Click the icon to view the table of integrals. 2/(a + bu)3 Jvarbuau= Juvarbudu = 2(3bu - 2a). The Gini index of income concentration is. 3b (Type an integer or decimal rounded to four decimal places as ne V(a+bu)3 15b? 2(15b²u? - 12abu + 8a) uVa+ bu du = V(a+bu)3 105b3 2va + bu du = Va + bu 2(bu - 2a) u du Va + bu Va+ bu 3b? 2(3b2u? - 4abu + 8a?) du = Va+bu Va + bu 15b3 Enter your answer in the answer box and then click Check Ar 1 -du = uva+ bu Va+ bu - va In Va Va + bu + Va a>0 All parts showingarrow_forward15. arc tag z dx x arc tag x - - In V1+z + c %3Darrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

