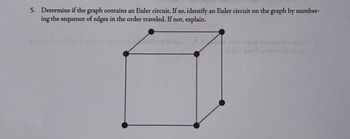
**Question 5: Euler Circuit Determination**Determine if the graph contains an Euler circuit. If so, identify an Euler circuit on the graph by numbering the sequence of edges in the order traveled. If not, explain.**Graph Description:**The graph is a representation of a cube. It consists of 8 vertices and 12 edges.- **Vertices:** Each vertex is placed at the corner of the cube structure.- **Edges:** Connect the vertices forming the cube shape. The edges connect in a 3D framework with four vertices on the top square face and four on the bottom square face.**Explanation:**To determine if the graph contains an Euler circuit, recall that an Euler circuit exists if all vertices have even degrees. In this graph:1. Each vertex is connected to 3 other vertices (since it’s a corner of a cube).2. Thus, each vertex has a degree of 3, which is odd.Since all vertices have odd degrees, the graph does **not** contain an Euler circuit.

Answered: 5. Determine if the graph contains an…

5. Determine if the graph contains an Euler circuit. If so, identify an Euler circuit on the graph by number- ing the sequence of edges in the order traveled. If not, explain. Ay the dog &#ibri &

Algebra and Trigonometry (6th Edition)

6th Edition

ISBN:9780134463216

Author:Robert F. Blitzer

Publisher:Robert F. Blitzer

ChapterP: Prerequisites: Fundamental Concepts Of Algebra

Section: Chapter Questions

Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...

See similar textbooks

Similar questions

4. Þescribe each graph below. Explain how many vertices and how many edges it has, and if it is a tree or not a tree. 10 Grapns E D Write your response below:
Does the following graph contain an Euler circuit? Explain why or why not.
Fill in the blank with the appropriate word. A connected graph has at least one Euler path that is also an Euler circuit, if the graph has A connected graph has at least one Euler path that is also an Euler circuit, if the graph has odd vertices. odd vertices. four
Find a Hamilton circuit for the graph that begins with the specific edge EA and AE
3) Determine whether the sequence of vertices is a path only, a circuit, or neither in the given graph. Circle the options listed in the part related to the given sequence. A B D E H a) BHFG b) BF G→C ⇒F→B c) GFH →B⇒F⇒C⇒G C PATH ONLY PATH ONLY PATH ONLY CIRCUIT CIRCUIT CIRCUIT NEITHER NEITHER NEITHER
The following graph has 9 vertices. a. Does this graph have an Euler circuit? Why? 22 21 12 b. Does this graph have an Euler path? Why? 20 02 10 01 c. Does this graph have a Hamilton path? Why? 00
1) Definitions. The graph below shows 5 cities. The weights on the edges represent the airfare for a one-way flight between the cities. a. How many vertices and edges does the graph have? b. Is the graph connected? c. What is the degree of the vertex representing LA? d. If you fly from Seattle to Dallas to Atlanta, is that a path or a circuit? And what is its cost? e. If you fly from LA to Chicago to Dallas to LA, is that a path or a circuit? And what is its cost? f. Is the graph a complete graph? If so, how many Hamiltonian circuits does it have? Seattle LA $100 $70 $150- $145 Chicago $170 $75 $120 $140 $165 $85 Atlanta Dallas
13. A mail person decides to park their vehicle and walk through one of the neighborhoods they deliver mail. They want to return to their vehicle without crossing any path twice. Can they get back to their vehicle using the graph K, below? Find the degrees of the vertices, then find an Euler circuit if one exists. h K9 Fill in the degree of each vertex based on the graph. Vertex Degree a b d e f g y Euler circuit:
The following graph has a Hamilton circuit. b d h
The graph shown has at least one Euler circuit. Determine an Euler circuit that begins and ends with vertex C. Complete the path so that it is an Euler circuit. C, A, B, E, D, A, 0 ... (.... D B E
6. Determine whether the given graph has an Euler circuit. Construct such a circuit when one exists. If no Euler circuit exists, determine whether the graph has an Euler path and construct such a path if one exists. Write the reason your answer is correct. Euler Circuit: Yes No Euler Path: Yes No b Ø d a Reason: Reason: Euler Path/Circuit: