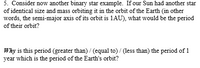
5. Consider now another binary star example. If our Sun had another star of identical size and mass orbiting it in the orbit of the Earth (in other words, the semi-major axis of its orbit is 1AU), what would be the period of their orbit? Why is this period (greater than) / (equal to) / (less than) the period of 1 year which is the period of the Earth's orbit?

ANY HELP WOULD BE APPRECIATED, THANKS

Can you answer problem 9? Can you also provide a short explanation for the answer you chose?

In the answer, it gives a formula f-ff=m(0) and afterwards simplies into 120 - ff = 0 and further into ff=120N. My question is how do you not have to divide by 0 to finish the equation if that makes sense. To simply further why are we able to ignore the m(0) portion?

1. ANALYTICAL METHOD OF ADDING VECTORS Solve the same problem as PART 1 but this time analytically. START with the values below. DO NOT USE VALUES FROM PART 1. Suppose you first walk A = 12 m in a direction 20° west of north and then B= 20 m in a direction 40° south of west. Let the +x-axis coincide with the easterly direction and the +y-axis with the northerly direction. Note: In this problem, do not round values if you need to use them for calculations in subsequent parts. Rounding errors can propagate and can make your final answer lie outside the tolerance limit of 5% set for this problem. Keep all answers to 4 significant figures.

Please answer the 3 subparts A,B,C with the step of solution, because i know the tutor can answer max 3 subparts . Thank u. ( Need In 60-120 minutes )

Here's how gym membership works for a potential customer: If the customer decides to join the gym, she will pay J on day 0. Then, she can use the gym starting the next day for 5 days (1; 2; 3; 4; 5), paying an additional F on each day she visits. If she goes to the gym on any given day, it costs her (10+ F) that day, but beneÖts her 30 the next day. In other words, her "costs" are a sum of her psychic costs (10) and actual Onancial costs (F). Assume that, when indi§erent, the individual will go to the gym. (a) Suppose the potential customer is a standard exponential discounter with a discount factor of = 12. If gym membership was free (i.e. J = 0 and F = 0) would she join the gym? If so, how many days would she actually go? (b) Suppose the gym did not charge a joining fee. How high could it set the usage fee? What would its revenues from this customer be? (c) Suppose instead the gym decided not to charge a usage fee. How high could it set the joining fee? [Hint: To Ögure out the…

Can you please solve problem 5, thanks!

Can you answer problem 6? Can you also provide a short explanation for the answer you chose?