On the map, let the +x-axis point east and the +y-axis north. An airplane flies at 880 km/h northwestward direction (i.e., midway between north and west). Can you help me visualize the components of the first velocity, and when the plane flies due south at the same velocity.
I understand the answer will be -622.25 for the run, meaning 880*cos(45) for x -axis; the y axis north is 880*sin(45) resulting in 622.5
Please help me visualize the first and second velocity when the plane flies due south at the same velocity? Help me to visualize where one of the velocities due south is zero, and the other is whatever it is.
I am afraid I can properly visualize or understand in simple terms what is asked. My point can you help to understand the right angle theorem to the angle.
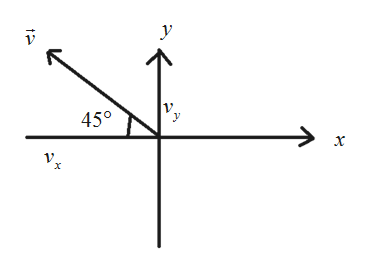
Draw the diagram of the velocity components with proper labeling.
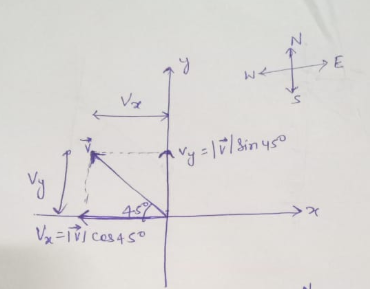
To reach to the components of the velocity along x-direction and y-direction. Use the right-angle triangle properties and the trigonometrical identity, and solve as:
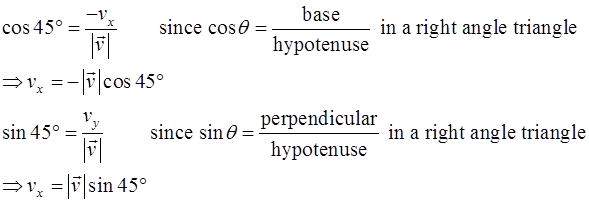
Therefore, the component along x-direction and y-direction is: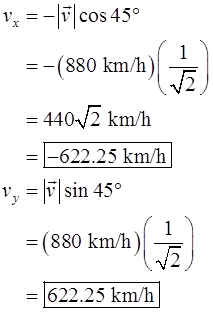
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images
