Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
Please follow how the example was given in the other photo to solve this LPP using simplex method. This was is easier and short for me to understand
![Put in Standform
Basic feascal Solution
To phase Method
Ex 2: Solve the LP problem weing the simplex
Method:
Max
84:
J
5x + 6x₂
S3x₁ + 4x₂ = 18
2x₁ + x₂ < 7
X₁, X270
Soln: 1st transform the LP problem into standard
form
bv
X3
X4
Construct the initial
Initial
min
5x - 6x₂
& √3x₁ + 4x₂ + x3 = 18
2x₁ + x₂ + x4 = 7
-х, ха, хз, х4 70
X₁
is NOI
-S
X₂
4
Current basis
XB =
b.f.s
1
-6
X3
1
O
Ⓒ
}
000円
tableau
X4
20-0
O
Using the
Simplex Metud
b
18
7
O
[93 94] = [0]
(₂=-6
min
~ { b², 9:₂>0} = min [18, +} = 2
The
two-phase Simplex Method
There are two times when an 4 probleem has no
starting bifis and thus, the simplex method canot
be readily initiated. Thus, there is a need to
a
systemic method to find
LP problem.
The
Two-
Method
an
require
Starting bifs to such
-phase
Such
method
Example: be the simplex method to solve
min
2x₁ + 3x₂
Slo: 1st
Sit
a
4x + 2x₂ > 12
X₁ + 4x₂ > 6
X₁, X₂ 70
transform
min
sit
9 which occurs in
row I
is
the
2x + 3x₂
4рх, +2х2 - Хз
- 12
X₁ + 4x₂ - X = 6
X₁, X2, X3, X470
problem in standard form :
There is
basis matrix since on the f.T-
no
for tp problem would imply there is a bifus. But
Such a Solution would have been (00X3 X4) ! But
X3 = -12 and Xq = -6
which is feasible.
none
of](https://content.bartleby.com/qna-images/question/79599c56-a340-49a0-b0ff-829b3947a798/4e448421-b01d-4d34-b2ff-ddd8e26e3cd4/vu8c2c_processed.jpeg)
Transcribed Image Text:Put in Standform
Basic feascal Solution
To phase Method
Ex 2: Solve the LP problem weing the simplex
Method:
Max
84:
J
5x + 6x₂
S3x₁ + 4x₂ = 18
2x₁ + x₂ < 7
X₁, X270
Soln: 1st transform the LP problem into standard
form
bv
X3
X4
Construct the initial
Initial
min
5x - 6x₂
& √3x₁ + 4x₂ + x3 = 18
2x₁ + x₂ + x4 = 7
-х, ха, хз, х4 70
X₁
is NOI
-S
X₂
4
Current basis
XB =
b.f.s
1
-6
X3
1
O
Ⓒ
}
000円
tableau
X4
20-0
O
Using the
Simplex Metud
b
18
7
O
[93 94] = [0]
(₂=-6
min
~ { b², 9:₂>0} = min [18, +} = 2
The
two-phase Simplex Method
There are two times when an 4 probleem has no
starting bifis and thus, the simplex method canot
be readily initiated. Thus, there is a need to
a
systemic method to find
LP problem.
The
Two-
Method
an
require
Starting bifs to such
-phase
Such
method
Example: be the simplex method to solve
min
2x₁ + 3x₂
Slo: 1st
Sit
a
4x + 2x₂ > 12
X₁ + 4x₂ > 6
X₁, X₂ 70
transform
min
sit
9 which occurs in
row I
is
the
2x + 3x₂
4рх, +2х2 - Хз
- 12
X₁ + 4x₂ - X = 6
X₁, X2, X3, X470
problem in standard form :
There is
basis matrix since on the f.T-
no
for tp problem would imply there is a bifus. But
Such a Solution would have been (00X3 X4) ! But
X3 = -12 and Xq = -6
which is feasible.
none
of
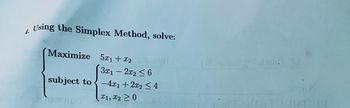
Transcribed Image Text:Using the Simplex Method, solve:
Maximize 5x1 + x2
3x12x26
subject to-4x1+2x2 ≤ 4
x1, x2 > 0
(10210 gast.
V
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images
Knowledge Booster
Similar questions
- Please help mearrow_forwardI need to simplifyarrow_forwardI am currently doing this equation 4x+13-{2x-[4(x-3)-5}=2x-12 Now I know I have to distribute to get rid of the symbols but the part that is tripping me up is the : -{2x-[4(x-3)-5} can you help explain to me how to do that part of the equation?arrow_forward
- Please help me solve for vertex and if up or downarrow_forwardI understand that so much better then the last person that helped. could you do the same thing but swap the equation out for -2x=8y instead of x=5arrow_forwardSuppose you are given a Rectangular piece of cardboard having length 3x-7 inches and width 5x+2 inches. Then you cut out a square from this piece of cardboard having side length x inches. Find the area of the remaining piece of cardboard expressed in terms of x. Please provide steps in detail and how you are thinking to get to a solution. Thank youarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,