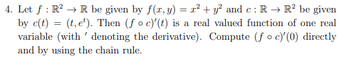
4. Let f: R² → R be given by f(x, y) = x² + y² and c: R → R² be given by c(t) = (t, e¹). Then (f o c)'(t) is a real valued function of one real variable (with denoting the derivative). Compute (foc)'(0) directly and by using the chain rule.

デジタル形式で段階的に解決 ありがとう!! SOLVE STEP BY STEP IN DIGITAL FORMAT 6. A small metal bar, whose initial temperature was 20°C, is dropped into a large container containing boiling water. How long will it take for the bar to reach 90°C if it is known that its temperature increased 5°C in a second?

Find y as a function of a if y(0) = 24, y' (0) = 16, y" (0) y(x) = y"7y" +12y = 6e*, = 27. =

Bracket Manufacturing uses a Kanban system for a component. Daily demand is 1,100 units. Each container has a combined waiting and processing time of 0.65 days. If the container size is 100 and the alpha value (a) is 12%, how many Kanban card sets should be authorized? Round your answer up to the whole number. Kanban card set(s) What is the maximum authorized inventory? Use the rounded value from the previous question. Round your answer to the nearest whole number. unit(s)