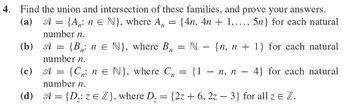
4. Find the union and intersection of these families, and prove your answers. (a) A = {A, ne N}, where A,, = {4n, 4n+ 1,..., 5n} for each natural number n. (b) A = {B: n = N), where B₁ = N. {n, n+1) for each natural number n. (c) A = {C₁; n = N}, where C = {1-n, n 4} for each natural - number n. (d) A = {D₂: ze Z}, where D₂ = {2z+6, 2z - 3} for all z € Z.

numbers of four digits can be formed with the digits 0, 1, 2, 3 (repetition of digits is How many not allowed? (a) 18 (b) 24

Number Theory

1. Assume that t is a particular integer. Use the definition of even, odd, or composite to justify the following. (a) 35 is an odd integer. (b) –14 is an even integer. (c) 77 is a composite integer. (d) 14t – 8 is an even integer. (e) 8t + 9 is an odd integer. 2. For all real numbers r, a? > 0. (a) Write the negation of the statement above. (b) Disprove the original statement by giving a counterexample.

For all natural numbers, P ( n , n ) = n ! True False

For each of the statements below (which all happen to be false), look atthe “proofs” that have been provided and explain in one or two sentences what error has been made by the author.

(a) The number N = 49,725 represents the ages of a group of teenagers multiplied together. How many teenagers are there and what are their ages? Explain. (b) Is there an integer N > 1 such that the square root, cube root, and fourth root of N are all integers, and if so, what is the smallest one?

Consider the list of numbers: 2n-1, where n first equals 2, then 3, 4, 5,6,…What is the smallest value of n for which 2n -1 is not a prime number.  Show all your work.

(9) How many different two-digit numbers can be made from the digits 3, 5 and 7 if: (a) the digits can be repeated? (b) the digits cannot be repeated? List all possibilities in each case.