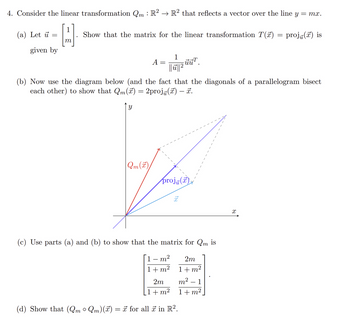
4. Consider the linear transformation Qm: R² → R² that reflects a vector over the line y = mx. [H]. Show that the matrix for the linear transformation T(T) = proj() is (a) Let u = given by (b) Now use the diagram below (and the fact that the diagonals of a parallelogram bisect each other) to show that Qm() = 2proj(x) - T. Y 1 A = uu¹ ||ū||² Qm (x) proj() (c) Use parts (a) and (b) to show that the matrix for Qm is [1 - m² - 2m 1+m² 1+m² 2m 1+m² (d) Show that (QmQm)(x) = for all in R². m² - 1 1+ m² X

Solve the problem. Let T: ²² be a linear transformation that maps u = · [1] into [3] Use the fact that T is linear to find the image of 3u+v. -8 28 -28 42 [] -36 [] 14 0 [11] -12 and maps v = · =[3] into [4]. ·

Find the matrix A of T. A= Consider a linear transformation T from R³ to R² for which = E T = [8]. T = T * (E) - · *(8) - · *(6) - A -H). =

2 [1], 0₂ = [1] · ₁ = [3], and y₂ = [¯ ] - 5 6 R² be a linear transformation that maps e₁ into y₁ and 19. Let e₁ = T: R² maps e2 into y2. Find the images of [3] -3 and [2]. x2 and let