
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN: 9781133382119
Author: Swokowski
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Question
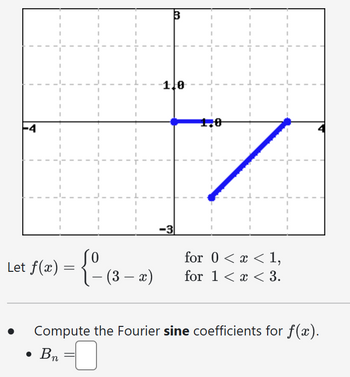
Transcribed Image Text:-4
m
1.0
1,0
0
Let f(x) = {º (3 - x)
•
-
-
-3
for 0 < x < 1,
for 1 < x < 3.
Compute the Fourier sine coefficients for f(x).
• Bn
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 12 images

Knowledge Booster
Similar questions
- Compute the derivative of the given function. sin ¹(x³ + 4) O O O d -[sin ¹(x³ + 4)] = dx d dx d dx d dx √ + 1-(-³ 4) 2 (x³ + 4) [sin ¹(x³ + 4)] = √/1 + (x² + 4)² (3x+²) +4)2 [sin¯¹(x³ + 4)] = = -[sin¯¹(x^³ + 4)] = 3x² 1 - (x³ + 4)² 1 1 – (x-³. (3x-²) +4)²arrow_forwardShow that d(w) ==}6(w − 1) +5(w+1)] is the Fourier transform of cos(t). - Show that d(w) = −ix[8(w − 1) − 8(w+1)] is the Fourier transform of sin(t).arrow_forwardConsider f(x) = xe The Fourier Sine transform of f(x) F,f(2) = The Fourier Cosine transform of f(x) Felf)(2) = Note that while we usually denote the transformed variable by a the transformed variable in this case is 21.arrow_forward
- PART D ONLY PLEASEarrow_forwardDetermine the transform of the following functions using any methods . t^2 sinh 3tarrow_forward10. Let f(x) = 2 cos(5.x)+3 sin(4x) and let q, be the Fourier polynomial of degree n for f. (a) Show that if n = 3, q,(x) = 0. (b) Find q4. (c) Explain why q„(x)= f(x) if n2 5.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage