Answered: 4) Determine the coordinates of the…

4) Determine the coordinates of the centroid of the shaded area in Figure 4 using Integration Method a) x b) y 4 Figure 4 y = √x 6 ft

Elements Of Electromagnetics

7th Edition

ISBN:9780190698614

Author:Sadiku, Matthew N. O.

Publisher:Sadiku, Matthew N. O.

ChapterMA: Math Assessment

Section: Chapter Questions

Problem 1.1MA

See similar textbooks

Related questions

Q: dimensions are: a=28m, b=17m and and c=2. Round off only on the final answer expressed in 3 decimal…

Q: Find the center of gravity M of the three dimensional homogeneous wire ABCD using the coordinate set…

Q: 54 44 (3 11 28 1) 46 ref 2) 17

A: This numerical is related to basic Centroid of composite area.

Q: A) Determine the area of the shaded region. B) Determine the y centroid for the shaded region. C)…

Q: F 0.12 m B 0.25 m 70 0.16 m F, -5 - 5 Î +j + ok kn ent due to force F around point O if played in…

Q: 10 *.Q1) A) Find the centroid location of the following shape y xp Э ст y = 9-x 9 cm 3 сm

A: Let us consider the elemental area dA=ydx determine the total shaded area

Q: s) What is the distance, d3x, of shape 3’s centroid from axis Xo? t) What is the distance, d6x, of…

A: The following table shows the centroid values of the various shapes presented in the given problem.…

Q: 25. What are the coordinates of the centroid C of the area shown? All dimensions are in mm 120 20…

Q: Part A- Locate the centroid C (x, y) of the shaded area of the following geometric shape

Q: a) Determine the second moment of area (IXX) about the centroidal x-axis for the solid homogeneous…

Q: This question is made of two parts: Part A-Locate the centroid C (x, y) of the shaded area of the…

Q: Given three vectors and their components as follows: Ā = (-4,2), B = (5,3), Č = (-6,3). Compute the…

Q: Locate the centrod.) of the shaded are Express your answers using three significant figures…

Q: 8. Determine the following a) Resultant of the force system b) x intercept c) x intercept ly. 340N…

Q: a D a A! y

A: Given data: The dimension a = 24 cm. The dimension b = 36 cm.

Q: Determine the centroid of the area shown below figure by the direct integration method.

Q: 5. What are the coordinates of the centroid of the area bounded by y = x² +2, x-axis (ory = 0), x =…

Q: A) Determine the area of the shaded region. B) Determine the y centroid for the shaded region. y y =…

Q: Find the center of gravity M of the three-dimensional homogeneous wire ABCD in the figure using the…

A: Given :- a = 24 cm b = 36 cm Find :- Coordinates for BC part = ?

Q: 04 Locate the centroid of the shaded area for the figure shown: Shape 1) a.x ay 4*9-36 72 b/3-9/3…

A: Centroid of an area is the point located in the area which is considered to be placed at an average…

Q: 4 Determine the centroid of the shaded area with Yes Pect to X-y axis- C all dimensions : in:mm) Y00…

Q: 3)→ Find-the-(x,y)-coordinates-of-the-centroid-for-the-shaded-shape-shown below:

A: Given:Shaded shape To find:X and Y coordinate of Centroid

Q: c) Calculate the first moment of area for the shape shown below about the axis s-s and find the…

Q: Solve for x and y components b. determine the magnitude and direction of the resultant c. Also…

Q: Determine the internal moment in kip-ft at the distance 14 ft. from point A (it is the point between…

Q: Part A-Locate the centroid C (x, y) of the shaded area of the following geometric shape

A: Given:

Q: Determine the following based on the given illustration: a) Area of the Composite figure b)…

Q: Determine the location of the centroid for the cross-section shown below and draw a scaled sketch of…

Q: a) X-coordinate of the centroid of the shape b) Y-coordinate of the centroid of the shape c) Second…

A: Note: According to Bartleby's guideline first three sub-parts are solved please upload other parts…

Q: The two rectangles in the figure below are each a by b cm. Determine the width b of the rectangles…

Q: v) What is the distance, d5y, of shape 5’s centroid from axis Yo? w) What is the distance, d2y, of…

A: (a) Consider the given section, (a) The centroid of the section 5 from Yo is,…

Q: "Determine the magnitude of resultant and its direction measured from Y- axis if a) FB- Goo and O=28…

Concept explainers

Center of Gravity and Centroid

The term center of gravity indicates the position or location of a point about which the whole weight of a body or system is supposed to be concentrated, which means the whole weight of the body or system works through this point. It is closely related to mass distribution. For all positions of the body, the center of gravity would be a single point.

Question

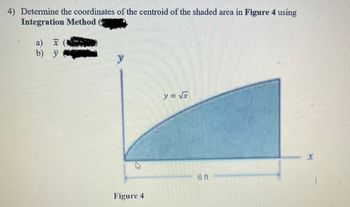
4) Determine the coordinates of the centroid of the shaded area in Figure 4 using
Integration Method
a) x
b)
y
Figure 4
y = √x

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1: Determine the curve equation

VIEW

Step 2: Calculate the coordinates of centroid

VIEW

Solution

VIEW

Step by step

Solved in 3 steps with 6 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.

Similar questions

Be sure to include units with your answers. Show your work. 40 mm X = Y = 60 mm 50 mm X 1) 8 pts) Find X for the centroid of the shape above. 2) 8 pts. Find Y of the shaded shape below. Ľ
a) A simply supported beam has a symmetrical rectangular cross-section. If the second moment of area (I) of a beam with a rectangular cross-section is11.50 x 106 mm4 about its centroidal x-axis and the depth dimension (d) of the rectangular section is 180 mm, determine the breadth dimension (b) for this beam section. Give your answer in millimetres (mm) and to 2 decimal places. Assume the beam section material is homogeneous. b) The same rectangular cross-section beam in Q2b is subjected to a maximum bending moment of 25,000 Nm and experiences sagging. Assuming that the centroidal axis passes through the beam section at (d/2), calculate the maximum bending stress (σmax) the beam will experience. Give your answer in N/mm2 and to 2 decimal places.
a) Determine the Area and the centroid of the shape. Show the calculations using integration. b) Find the Area Moment of Inertia about the X-axis using integration. Then find the Area Moment of Inertia about the x-x centroidal axis (x-bar) using the Parallel Axis Theorem. 2.0 in c) Find the Area Moment of Inertia about the Y-axis using integration. Then find the Area Moment of Inertia about the y-y centroidal axis (y-bar) using the Parallel Axis Theorem. 2.0 in
Locate the centroid y bar of the area in Figure 2. y =x 23 4 in. 8 in. Figure 2 Answer the following questions. b) Write the centroid formula for this problem. c) Apply the above formula to find the y - component of the centroid(dx).
Determine the (x, y) coordinates of the centroid of the shaded area shown in the figure below.
A rack is made from roll-formed sheet steel and has the cross section shown. Determine the location (x, y) of the centroid of the cross section. The dimensions are indicated at the center thickness of each segment. y -30 mm- 5 A) 15 mm 4 B) 7,5 mm 80 mm C) 0 mm 50 mm D) 5 mm 1 7 E) 10 mm 15 mm 15 mm 2KL 15* x, +50* x, +15*x, + 30 * x +30 *: x; +80* x6+15 *x, X = 235 X3 = ? 3. 2.
find the Y coordinate of the centroid of the composite line shown
For the plan area shown in the figure, determine the location of the centroid of the shaded area. Use matrix (table) method Use your last two digits for the triangle base side length Le m. .m 4 m 2 m 10 m 4 m 9m L=87m
b 17 Q 3) Locate the centroid of the shaded area shown in fig. all * . dimension in cm
Q.1) Determine coordinates of centroid of the shaded area shown in figure. All dimensions are 200 in mm. 80 40 40 20 300
It is designed in such a way that the internal temperature of a commercial heat treatment furnace can reach up to 165 oC. All surfaces of the furnace consist of firebrick (10 cm), insulation material and sheet metal (3mm) from the inside out. Given that the outdoor temperature is 22 oC, the outer sheet will be allowed to go up to 35 oC, which is a temperature that will not disturb in contact with hands. In this case, determine the insulation material thickness to be used. The thermal conductivity coefficient of the insulation material is insulation 0.066 W / m oC, 60 W / m oC for sheet metal and 115 W / m oC for firebrick. Indoor heat transfer coefficient will be accepted as 25 W / m2 oC and 12 W / m2 oC for outdoor environment.
Compute the coordinates of the centroid (,) of the area shown. Also compute the area moment of intertia about the x' and y' axes with origin at the centroid. ур C + 2013 Michael Swanbom cc 10 BY NC SA a*b* - a a → x Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 41 cm b 25 cm с 50 cm The x coordinate of the centroid is = cm. The y coordinate of the centroid is y cm. The moment of inertia about the x' axis going through the centroid is I' The moment of inertia about the y' axis going through the centroid is I✓ cm4. cm4.